Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL AND CAPACITANCE
MODERN PUBLICATION|Exercise Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)|10 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
MODERN PUBLICATION|Exercise Revision Exercises (Very Short Answer Questions)|56 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
MODERN PUBLICATION|Exercise NCERT FILE Solved (Exemplar Problems) (Very Short Answer Type Questions)|5 VideosELECTROMAGNETIC WAVES
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|14 VideosMAGNETISM AND MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|16 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE -NCERT FILE Solved (Exemplar Problems) (Short Answer Type Questions)
- Prove that a closed equipotenitial surface with no charge within itsel...
Text Solution
|
- A capacitor has some dielectric between its plates, and the capacitor ...
Text Solution
|
- Prove that, if an insulated, uncharged conductor is placed near a ch...
Text Solution
|
- Calculate potential energy of a point charge -q placed along the axis...
Text Solution
|
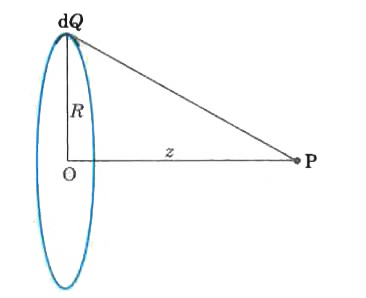
- Calculate potential on the axis of a ring due to charge Q uniformly ...
Text Solution
|