Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
RELATIONS AND FUNCTIONS
CENGAGE|Exercise Exercise 1.7|5 VideosRELATIONS AND FUNCTIONS
CENGAGE|Exercise Exercise 1.8|9 VideosRELATIONS AND FUNCTIONS
CENGAGE|Exercise Exercise 1.5|5 VideosQuadratic Equations, Inequalities, Modulus and Logarithms
CENGAGE|Exercise Question Bank|31 VideosSCALER TRIPLE PRODUCTS
CENGAGE|Exercise DPP 2.3|11 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-RELATIONS AND FUNCTIONS-Exercise 1.6
- Find the domain of f(x)=sqrt(sinx)+sqrt(16-x^2)
Text Solution
|
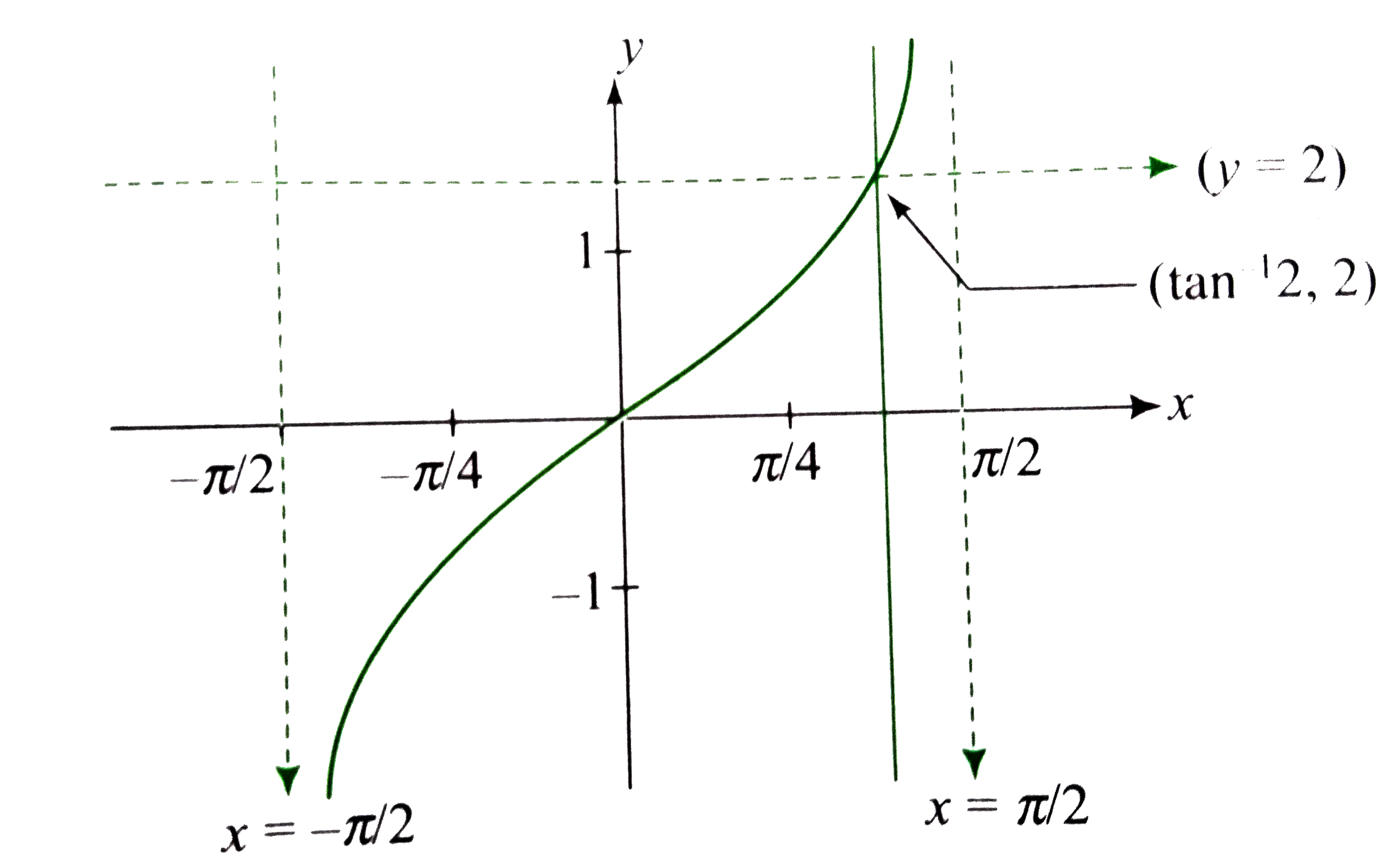
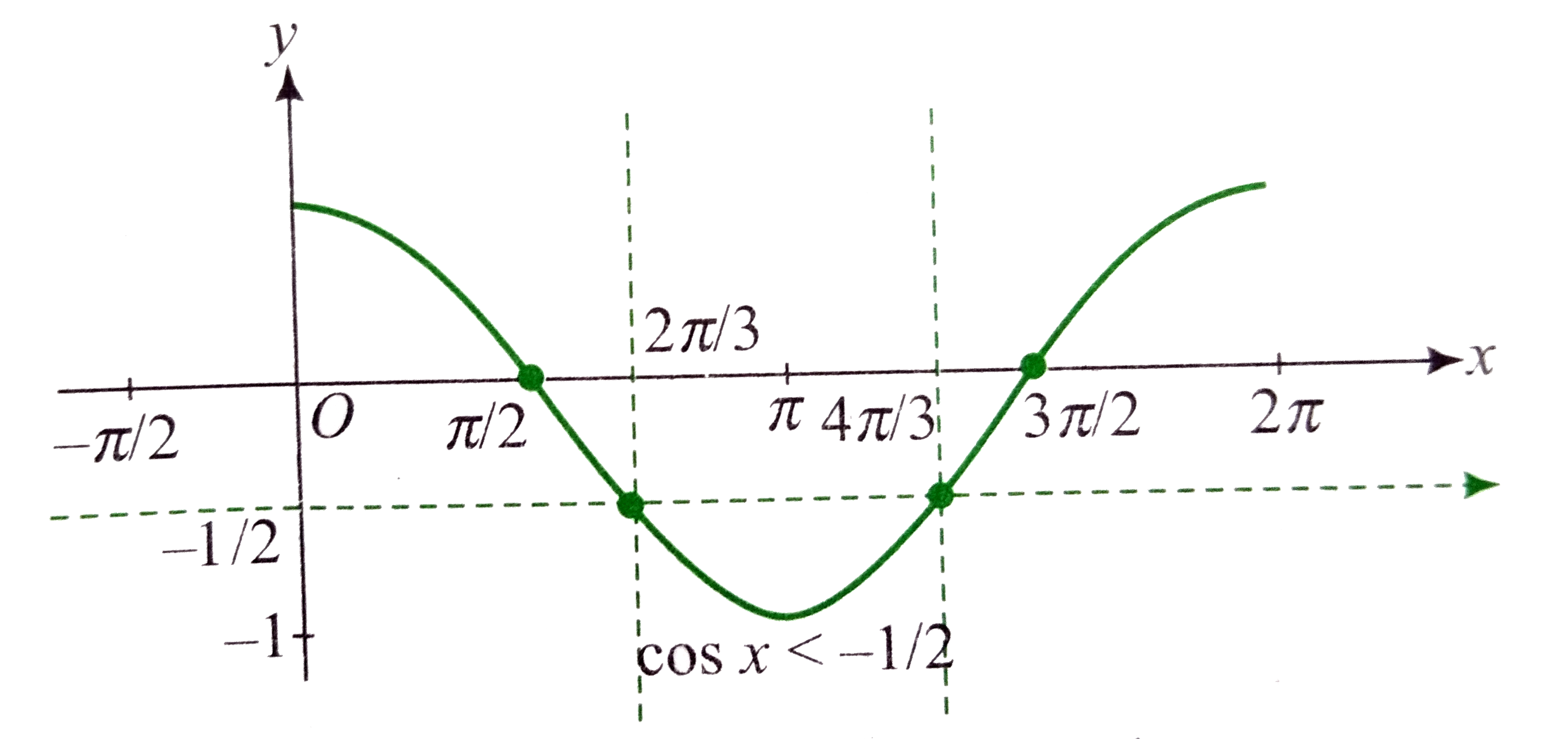
- Solve (a) tanx<2 cosxlt=-1/2
Text Solution
|
- Prove that the least positive value of x , satisfying tanx=x+1,l i e s...
Text Solution
|
- Find the range of f(x)=sec(pi/4cos^2x), where x in R
Text Solution
|
- If x in [1,2] , then find the range of f(x)=tanx
Text Solution
|
- Find the range of f(x)=1/(1-3sqrt(1-sin^2x))
Text Solution
|
- Find the range of f(x)=(2sin^2x+2sinx+3)/(sin^2x+sinx+1)
Text Solution
|
- Draw the graph of y=(sin2x)sqrt(1+tan^2x) , find its domain and range.
Text Solution
|