Find the area of the region bounded by the curves `y=sqrt(x+2) and y=(1)/(x+1)` between the lines x=0 and x=2.

Explanation

`y=sqrt(x+2)" ...(1)"`
`therefore" "y^(2)=x+2`
So, curve (1) is parabola for `ygt0.`
`y=(1)/(x+1)" ...(2)"`
`underset(xrarr-I^(+))lim(1)/(x+1)=oo and underset(xrarroo)lim(1)/(x+1)=0`
`y(0)=1.`
Also, y is decreasing function

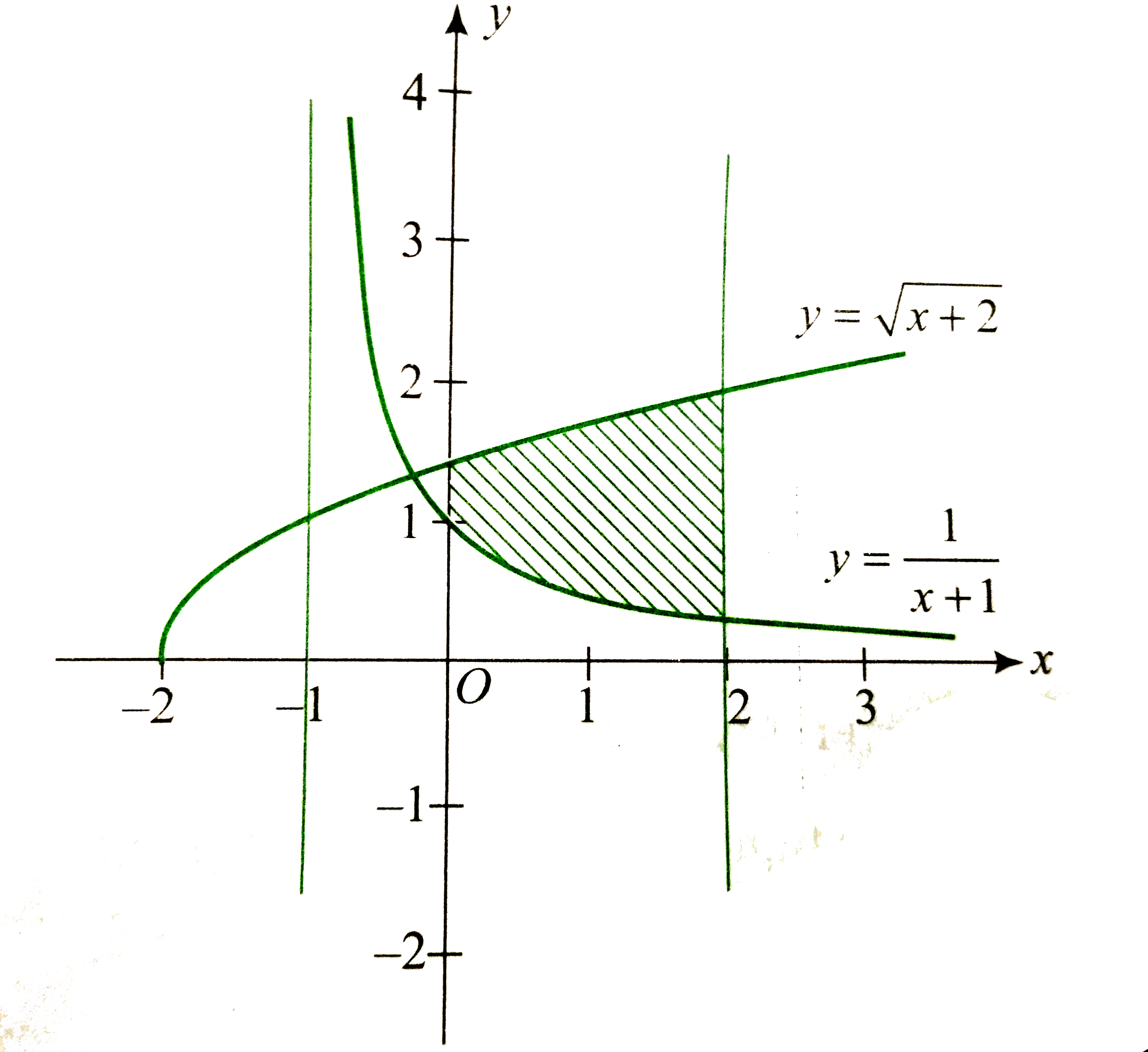
From the figure required area is
`A=overset(2)underset(0)int(sqrt(x+2)-(1)/(x+1))dx`
`=[(2)/(3)(x+2)^(3//2)-log_(e)(x+1)]_(0)^(2)`
`=((2)/(3)xx8-log_(e)3)-((2)/(3)xx2^(3//2)-log_(e)1)`
`=(16-4sqrt(2))/(3)-log_(e)3`