For `y^(2)le 4x,` points lie on or inside parabola `y^(2)=4x` for `x^(2)+y^(2)ge2x`, points lie on or outside circle `(x-1)^(2)+(y-0)^(2)=1" For "xle y+2,` points lie on or to the left side (towards origin) of the line x=y+2.
The graphs of the curves is as shown in the figure.
Solving parabola and line y=x+2, we get
`(x-2)^(2)=4x`
`"or "x^(2)-8x+4=0`
`"or "x=(8pmsqrt(48))/(2)=2(2pmsqrt(3))=(1pmsqrt(3))^(2)`
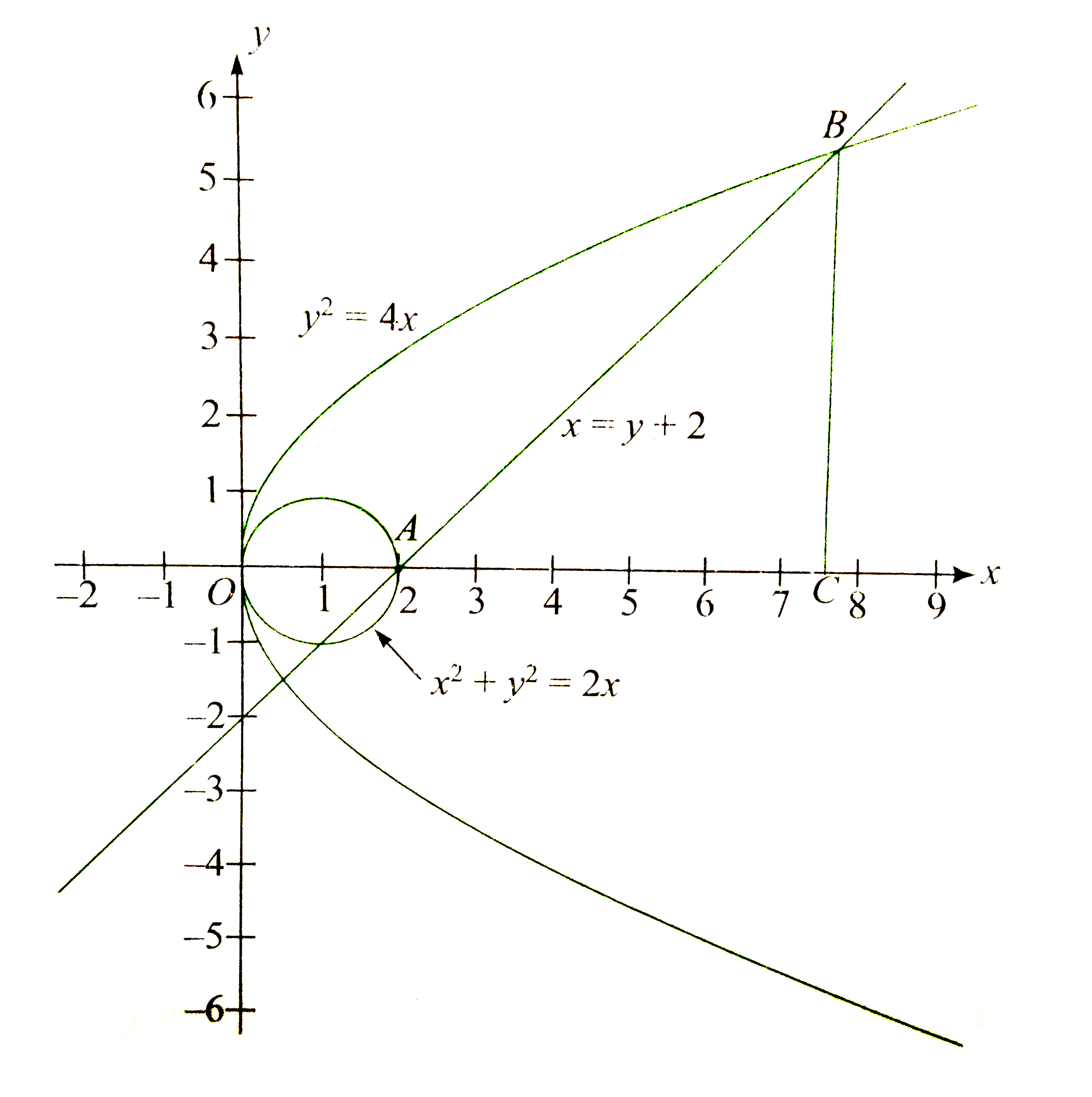
From the figure, required area is
`A=overset((sqrt(3)+1)^(2))underset(0)intsqrt(4x)d x-"Area of semicircle "`
`=sqrt(4)[(2x^(3//2))/(3)]_(0)^((sqrt(3)+1)^(2))-(pi)/(2)-(1)/(2)((sqrt(3)+1)^(2)-2)2(sqrt(3)+1)`
`=(4(sqrt(3)+1)^(3))/(3)-(pi)/(2)-2(sqrt(3)+1)^(2)`