Solving given curve, we have
`-x^(3)+x^(2)+16x=4x`
`therefore" "x=0 or x^(2)-x-12=0`
`rArr" "x=0 or (x-4)(x+3)=0`
`rArr" "x=0 or x=-3,4`
`"Now "y=-x^(3)+x^(2)+16`
`=-x(x^(2)-x-16)`
`"If "y=0" then "x=0 or x^(2)-x-16=0`
`therefore" "x=0 or x(1pmsqrt(65))/(2)`
From the above in information we having following graphs.
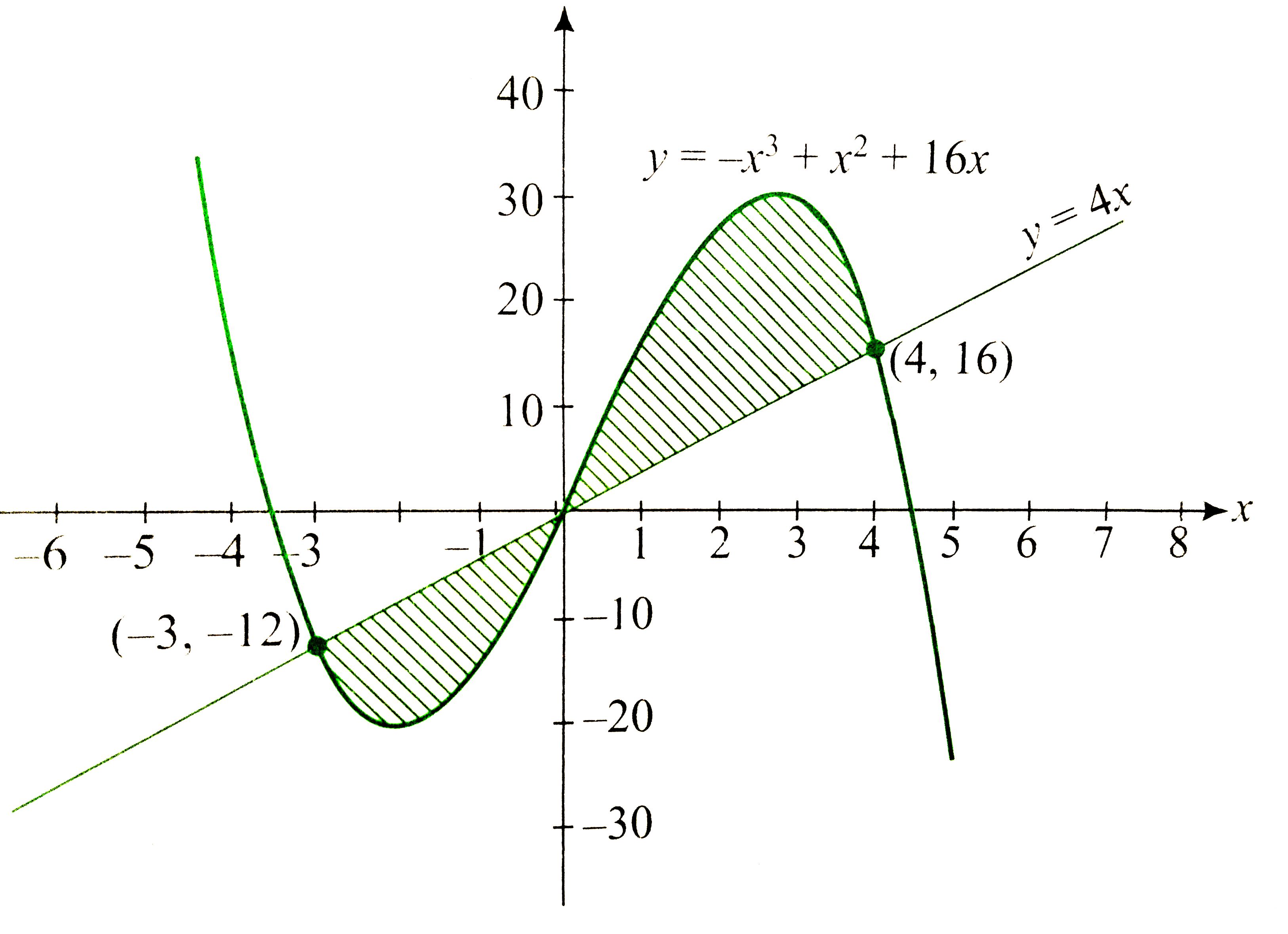
From the figure area of the shaded region,
`A=overset(0)underset(-3)int[4x-(-x^(3)+x^(2)+16x)]dx+overset(4)underset(0)int[(-x^(3)+x^(2)+16x)-4x]dx`
`=overset(0)underset(-3)int(x^(3)-x^(2)-12x)dx+overset(4)underset(0)int(-x^(2)+x^(2)+12x)dx`
`=[(x^(4))/(4)-(x^(3))/(3)-6x^(2)]_(-3)^(0)+[-(x^(4))/(4)+(x^(3))/(3)+6x^(2)]_(0)^(4)`
`=[-(81)/(4)-9+54]+[-64+(64)/(3)+96]`
`=(937)/(12)` sq. units.