Home
Class 12
MATHS
If the area bounded by f(x)=sqrt(tan x),...

If the area bounded by `f(x)=sqrt(tan x), y=f(c), x=0 and x=a, 0ltcltalt(pi)/(2)` is minimum then find the value of c.

Text Solution

Verified by Experts

Graph of `f(x)=sqrt(tan x)` is as shown in the following figure.

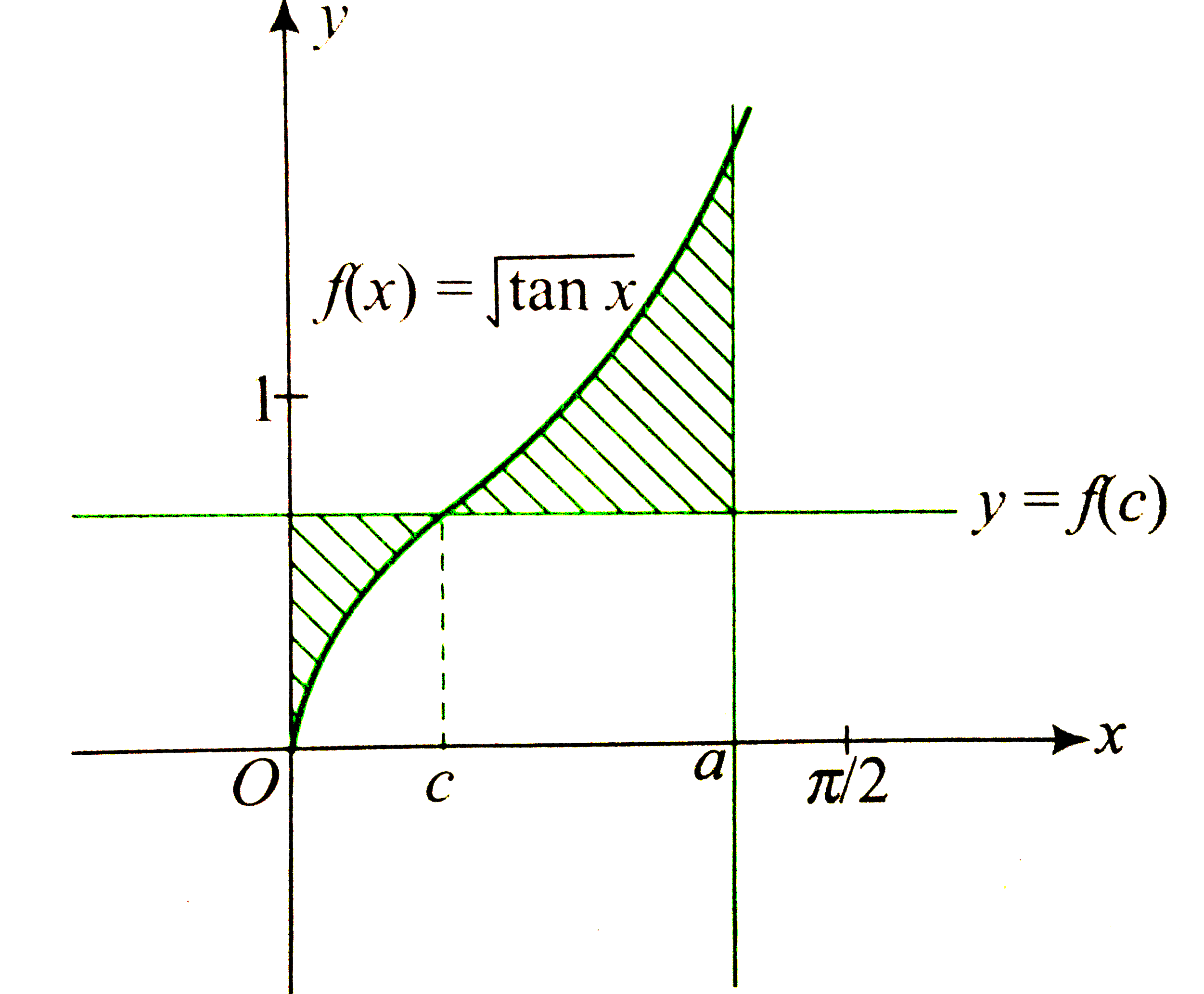
Required area is
`A=overset(c)underset(0)int(f(c)-f(x))dx+overset(a)underset(c)int(f(x)-f(c))dx`
`=overset(c)underset(0)intsqrt(tan c)dx-overset(c)underset(0)intsqrt(tan x )dx +overset(a)underset(c)intsqrt(tan x)dx-overset(a)underset(c)intsqrt(tan c)dx`
`=(2c-a)sqrt(tan c)-overset(c)underset(0)intsqrt(tan x)dx +overset(a)underset(c)intsqrt(tan x)dx`
`therefore" "(dA)/(dc)=2sqrt(tan c)+(2c-a)(sec^(2)c)/(2sqrt(tan c))-sqrt(tan c)-sqrt(tan c)`
`=(2c-a)(sec^(2)c)/(2sqrt(tan c))`
`(dA)/(dc)=0rArrc=(a)/(2)`
`"At "c=(a)/(2), (dA)/(dc)` changes sign from negative to positive
Hence A is minimum when `c=(a)/(2)`
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE|Exercise Exercise 9.1|9 Videos

  • AREA

    CENGAGE|Exercise Exercise 9.2|14 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE|Exercise Question Bank|29 Videos

  • AREA UNDER CURVES

    CENGAGE|Exercise Question Bank|20 Videos

Similar Questions

Explore conceptually related problems

If area bounded by f(x)=sin(x^(2)) with x axis,from x=0 to x=sqrt((pi)/(2)) is A,then

The area bounded by y=tan x,y=cot x,x axis in 0<=x<=(pi)/(2) is

Find the area bounded by y=1+2 sin^(2)x,"X-axis", X=0 and x=pi .

Find the area bounded by the y-axis,y=cos x, and y=sin x when 0<=x<=(pi)/(2)

If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2) . "Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx =f(c)(c-a)-int_(a)^(c)(f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c) rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx Differentiating w.r.t. c, we get (dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0) For maxima and minima , (dA)/(dc)=0 rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0) Hence, c=(a+b)/(2) "Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0 Hence, A is minimum when c=(a+b)/(2) . If the area bounded by f(x)=(x^(3))/(3)-x^(2)+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is

Find the area bounded by y = sin x and axis of x in (0 , pi)

If f(x)=1+cos x and g(x)=(a)/(bx^(2)+cx+1) If (0)=g(0),f'(0)=g'(0),f''(0)=g''(0) and the area bounded by the graph of g(x) and x-axis is k pi then find the value of k.

If the area bounded by y=f(x), the x -axis, the y-axis and x=t(t>0) is t^(2), then find f(x) .

If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2) . "Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx =f(c)(c-a)-int_(a)^(c) (f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c) rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx Differentiating w.r.t. c, we get (dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0) For maxima and minima , (dA)/(dc)=0 rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0) Hence, c=(a+b)/(2) "Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0 Hence, A is minimum when c=(a+b)/(2) . If the area enclosed by f(x)= sin x + cos x, y=a between two consecutive points of extremum is minimum, then the value of a is

Consider f(x)= minimum (x+2, sqrt(4-x)), AA x le 4 . If the area bounded by y=f(x) and the x - axis is (22)/(k) square units, then the value of k is