Find the area bounded by the curve `f(x)=x+ sin x and ` its inverse function between the ordinates `x=0" to "x=2pi`.

Explanation

`y=x+ sin x`
`therefore" "(dy)/(dx)=1+os x ge 0 AA x`
`"Also "(d^(2)y)/(dx^(2))=-sin x =0" when "x=npi, n in Z`
Hence `x= npi` are points of inflection, where curve changes its concavity.
`"Also, for "x in (0,pi), sin x gt 0 rArr x + sin x gt x`
`"And for " x in (pi, 2pi), sin x lt 0 rArr x + sin x lt x`
Thus, we have following graphs of function y=f(x) and its inverse function.

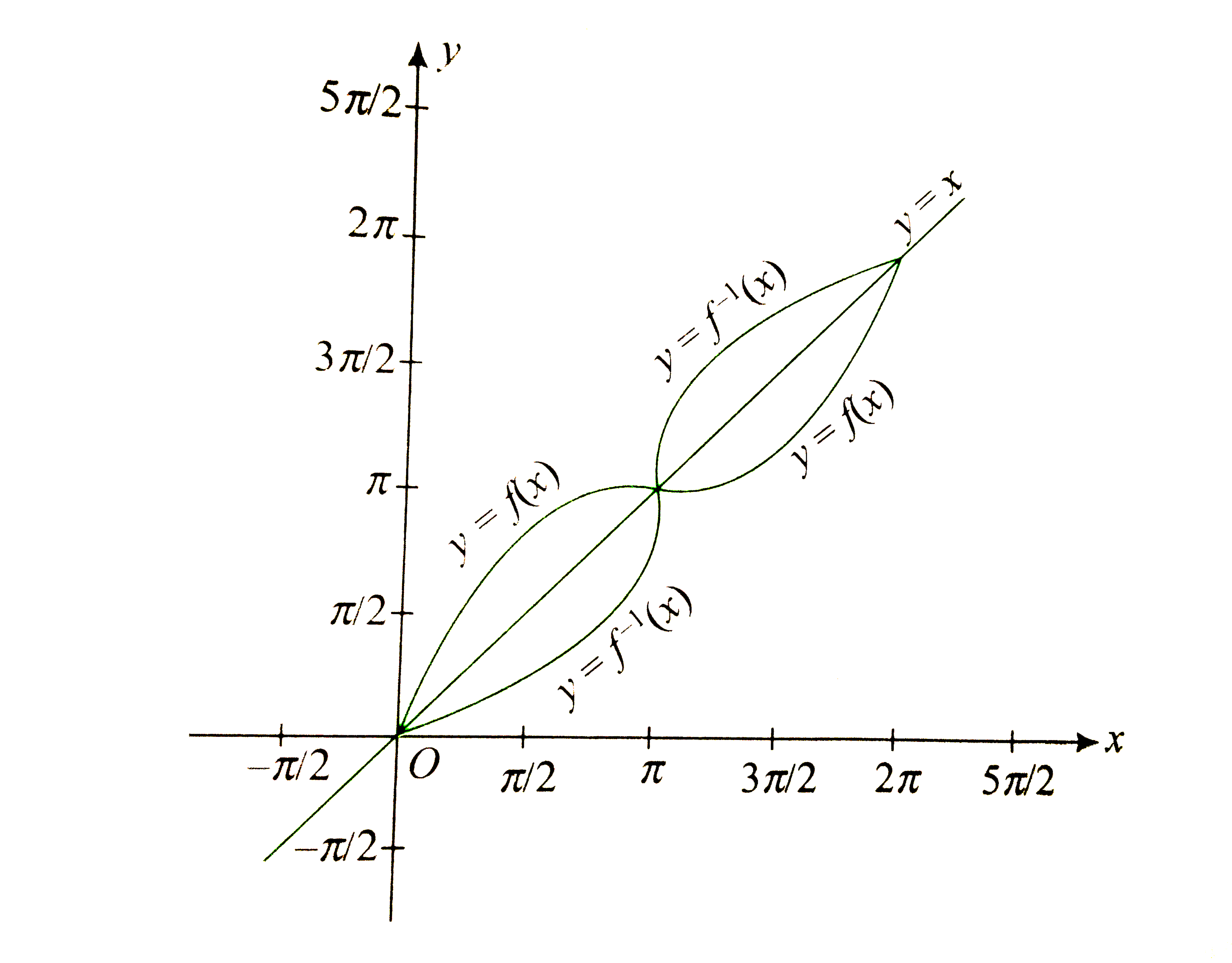
`"Required area "=4int_(0)^(pi)(f(x)-x)dx`
`=4int _(0)^(pi)sin x dx = 4xx2=8` sq. units.