The given curves are
`x^(2)=y" (1)"`
`x^(2)=-y" (2)"`
`y^(2)=4x-3" (3)"`
Clearly (1) and (2) meet at (0,0).
Solving (1) and (3), we get `x^(4)-4x+3=0`
`"or "(x-1)(x^(3)+x^(2)+x-3)=0`
`"or "(x-1)^(2)(x^(2)+2x+3)=0`
`rArr" "x=1 rArr y=1`
Thus, point of intersection is (1,1)
Similarly, point of intersection of (2) and (3) is (1,-1).
The graphs of three curves are as shown in the figure.
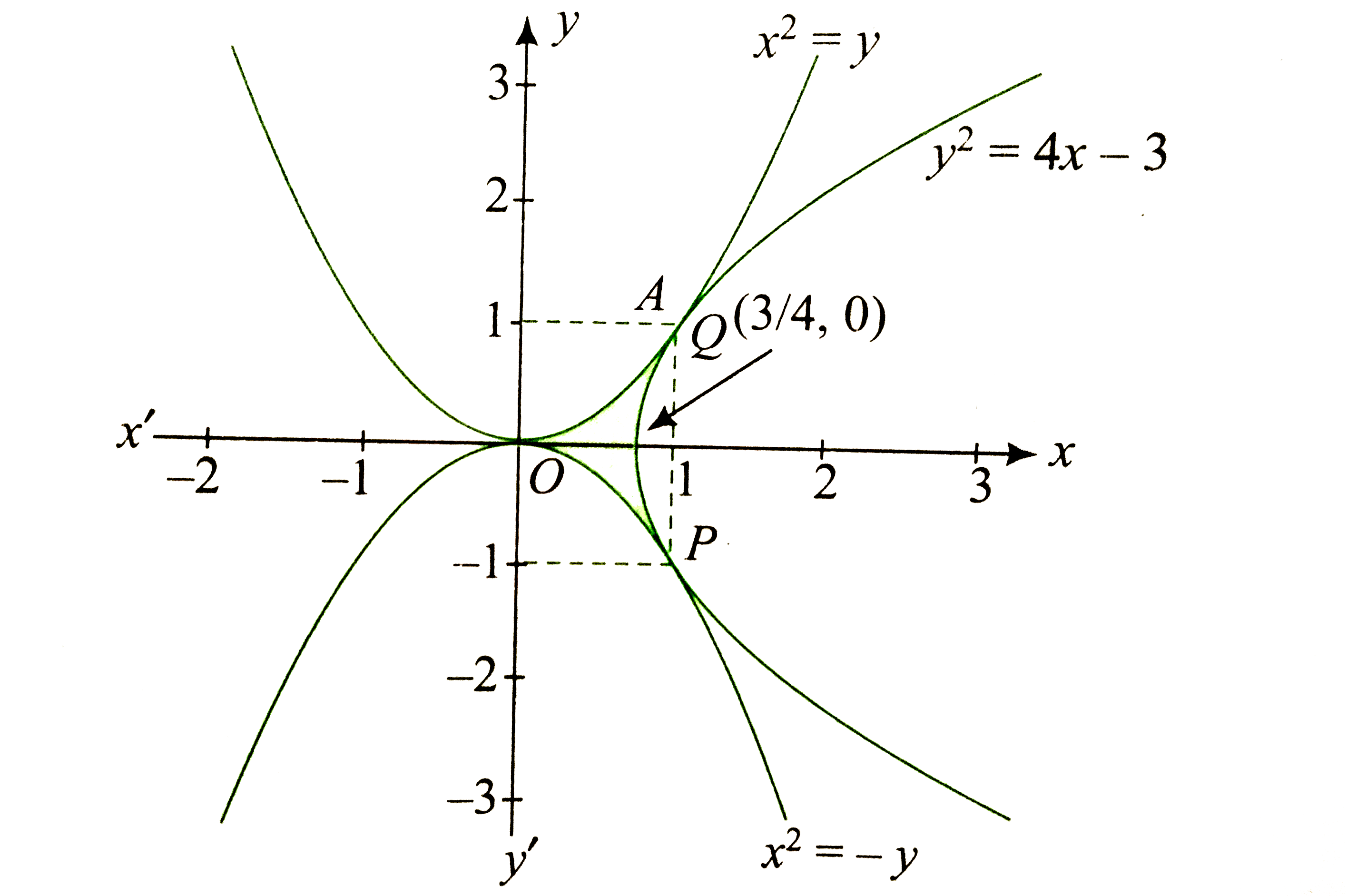
We also observe that at `x=1 andy y=1, (dy)/(dx)" for "(1) and (3)` is same
and hence the two curves touch each other at (1,1).
Same is the case with (2) and (3) at (1,-1).
Required area = Shaded region in the figure
`=2(Ar" "OPQA)`
`2[int_(0)^(1)x^(2)dx-int_(3//4)^(1)sqrt(4x-3)dx]`
`=2[((x^(2))/(3))_(0)^(1)-((2(4x-3)^(3//2))/(4xx3))_(3//4)^(1)]=2[(1)/(3)-(1)/(6)]`
`=(1)/(3)` sq. units.