Find the area of the region bounded by the curves `y=x^2,y=|2-x^2|,a n dy l=2,` which lies to the right of the line `x=1.`

Explanation

The given curves are
`y=x^(2)" (1)"`
`y=|2-x^(2)|" (2)"`
The graphs of these curve are as follows :

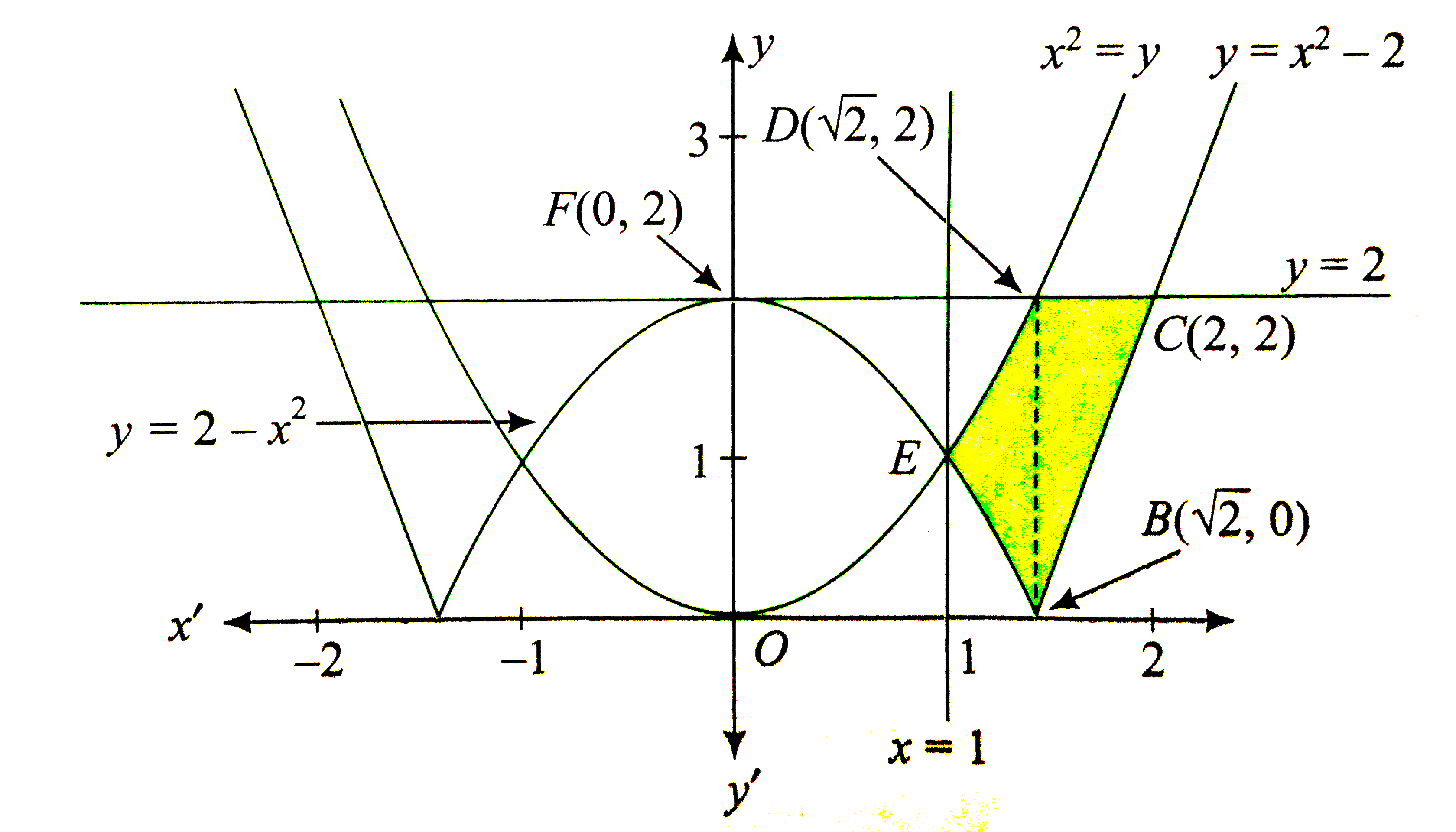
`therefore" Required area "=BCDEB`
`=int_(1)^(sqrt(2))[x^(2)-(2-x^(2))]dx+int_(sqrt(2))^(2)[2-(x^(2)-2)]dx`
`=int_(1)^(sqrt(2))(2x^(2)-2)dx+int_(sqrt(2))^(2)(4-x^(2))dx`
`=[(2x^(3))/(3)-2x]_(1)^(sqrt(2))+[4x-(x^(3))/(3)]_(sqrt(2))^(2)`
`=((4sqrt(2))/(3)-2sqrt(2)-(2)/(3)+2)+(8-(8)/(3)-4sqrt(2)+(2sqrt(2))/(3))`
`=((20)/(3)-4sqrt(2))` sq. units.