`"We have "2x+1=sqrt(4y+1)" ...(1)"`
`"or "(2x+1)^(2)=4y+1`
`"or "y=x^(2)+x" ...(2)"`
`therefore" Curve (1) is part of the parabola (2), for " x ge - 1//2`.
Differentiating (2), w.r.t. x, we get
`(dy)/(dx)=2x+1`
`therefore" "((dy)/(dx))_(x=0)=1.`
`therefore" "` line y=x is tangent to curve (2) at (0,0).
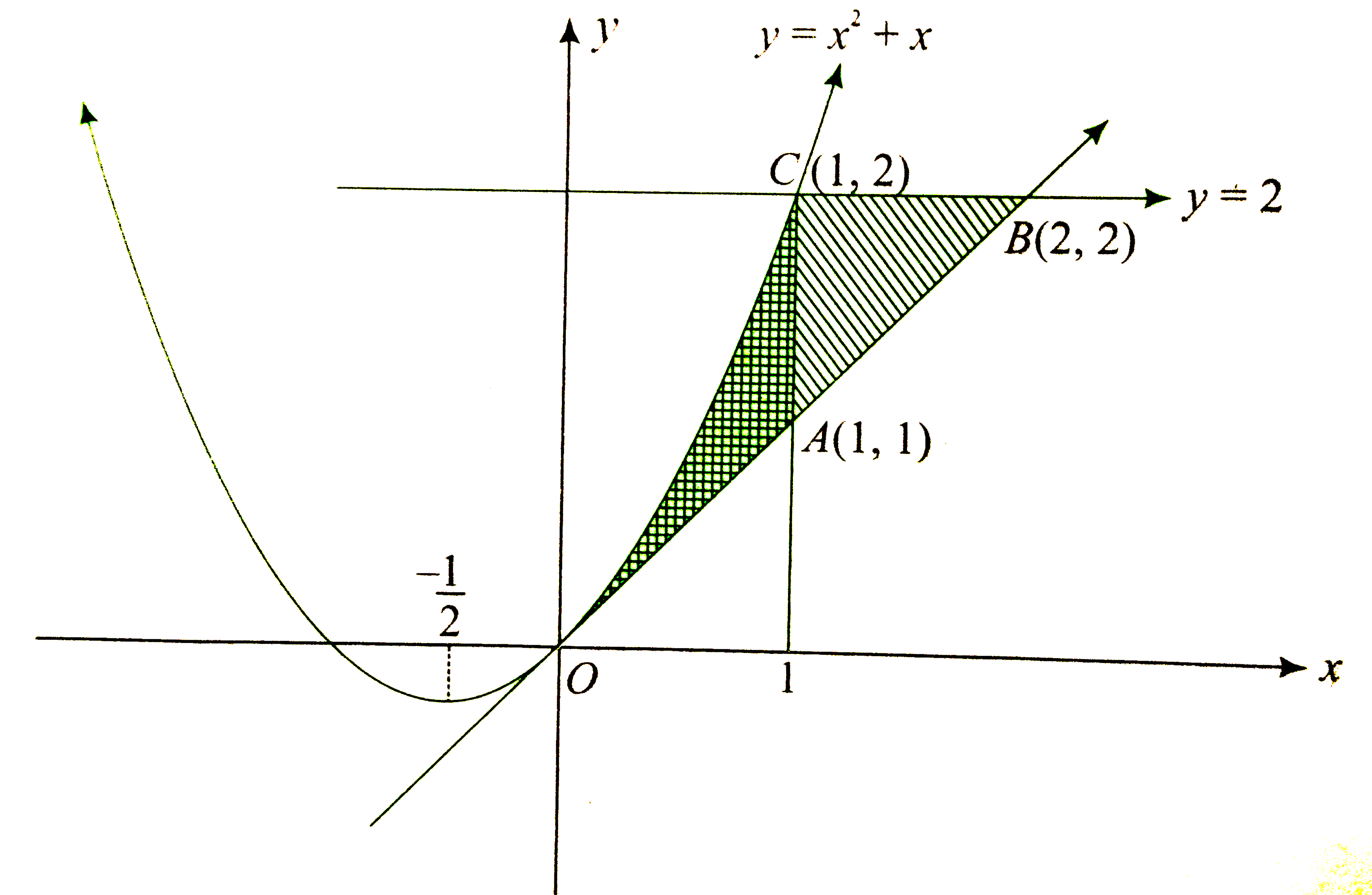
From the figure,
`"Area of the region "OACO is =overset(1)underset(0)int(x^(2)+x-x)dx`
`=[(x^(3))/(3)]_(0)^(1)=(1)/(3)`
`"Area of the triangle "ACB is =(1)/(2)xx1xx1=(1)/(2)`
`therefore" Required ratio "=(1//3)/(1//2)=(2)/(3)`