The given curve is `y= tan x" (1)"`
`"When "x=pi//4, y=1`
i.e., co-ordinates of P are `(pi//4,1)`
`therefore" equation of tangent at P is "y-1=(sec^(2)""(pi)/(4))(x-pi//4)`
`"or "y=2x+1 - pi//2`
The graphs of (1) and (2) are as shown in the figure.
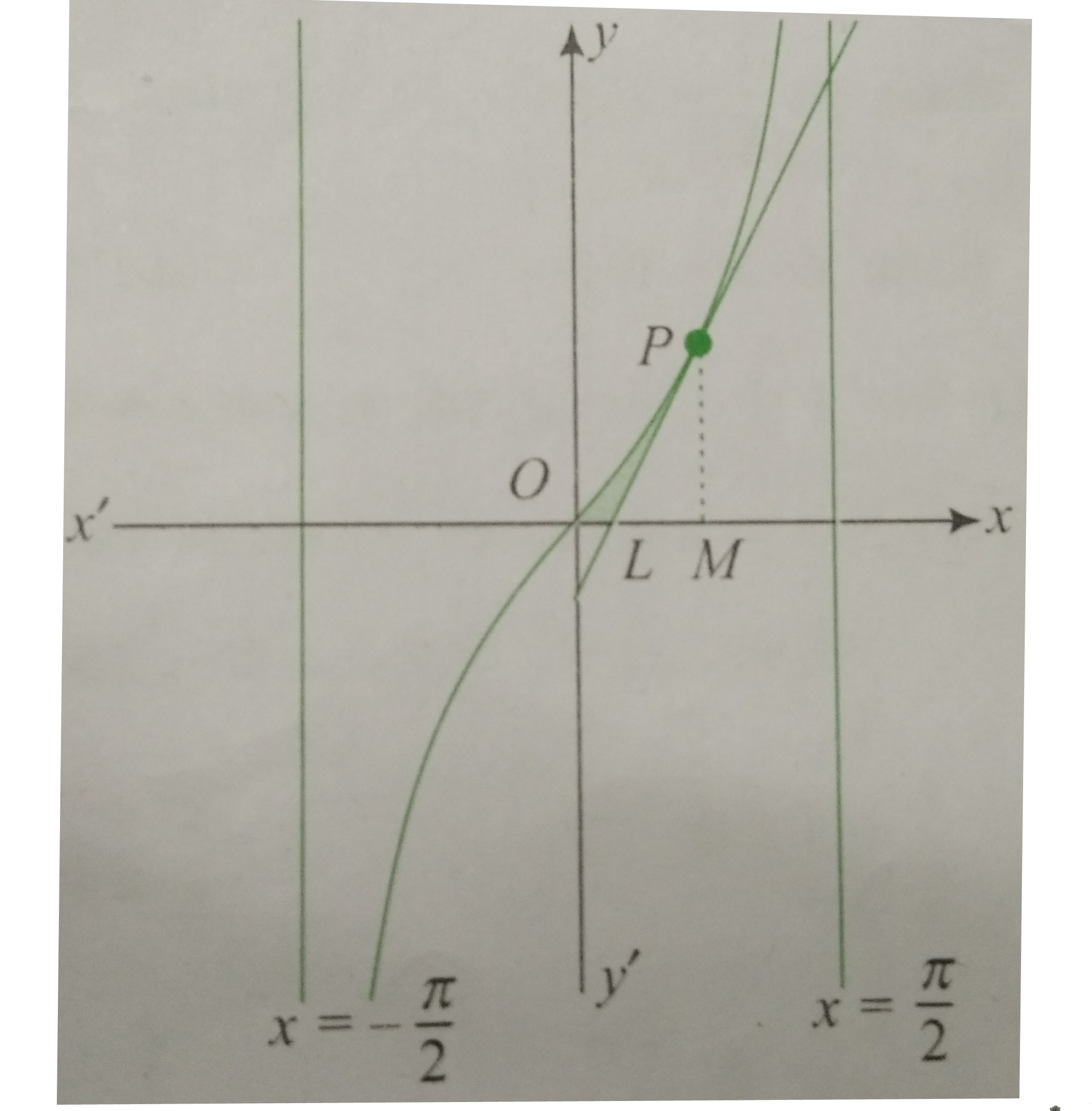
`"Tangent (2) meets x-axis at "L((pi-2)/(4),0)`
Now, Required area =Shaded area
`="Area "OPMO-Ar (Delta PLM)`
`=int_(0)^(pi//4)tan x dx -(1)/(2) (OM-OL)PM`
`=[log sec x ]_(0)^(pi//4)-(1)/(2)xx{(pi)/(2)-(pi-2)/(4)}xx1`
`=(1)/(2)[ log 2 -(1)/(2)]sq. units.