The given curves are
`y=ex log_(e) x" (1)"`
`y=(log x)/(ex)" (2)"`
The two curves intersect where `ex log x =(log x)/(ex)`
`rArr" "(ex -(1)/(ex))log x =0 rArr x = (1)/(e) or x=1`
`"At "x=1//e, y=-1 ("from"(1))`
`"At "x=1, y=0 ("from"(1))`
So points of intersection are `((1)/(e),-1) and (1, 0).`

From the above information, the rough sketch of two curves is as shown in the figure and the shaded area is the required area.
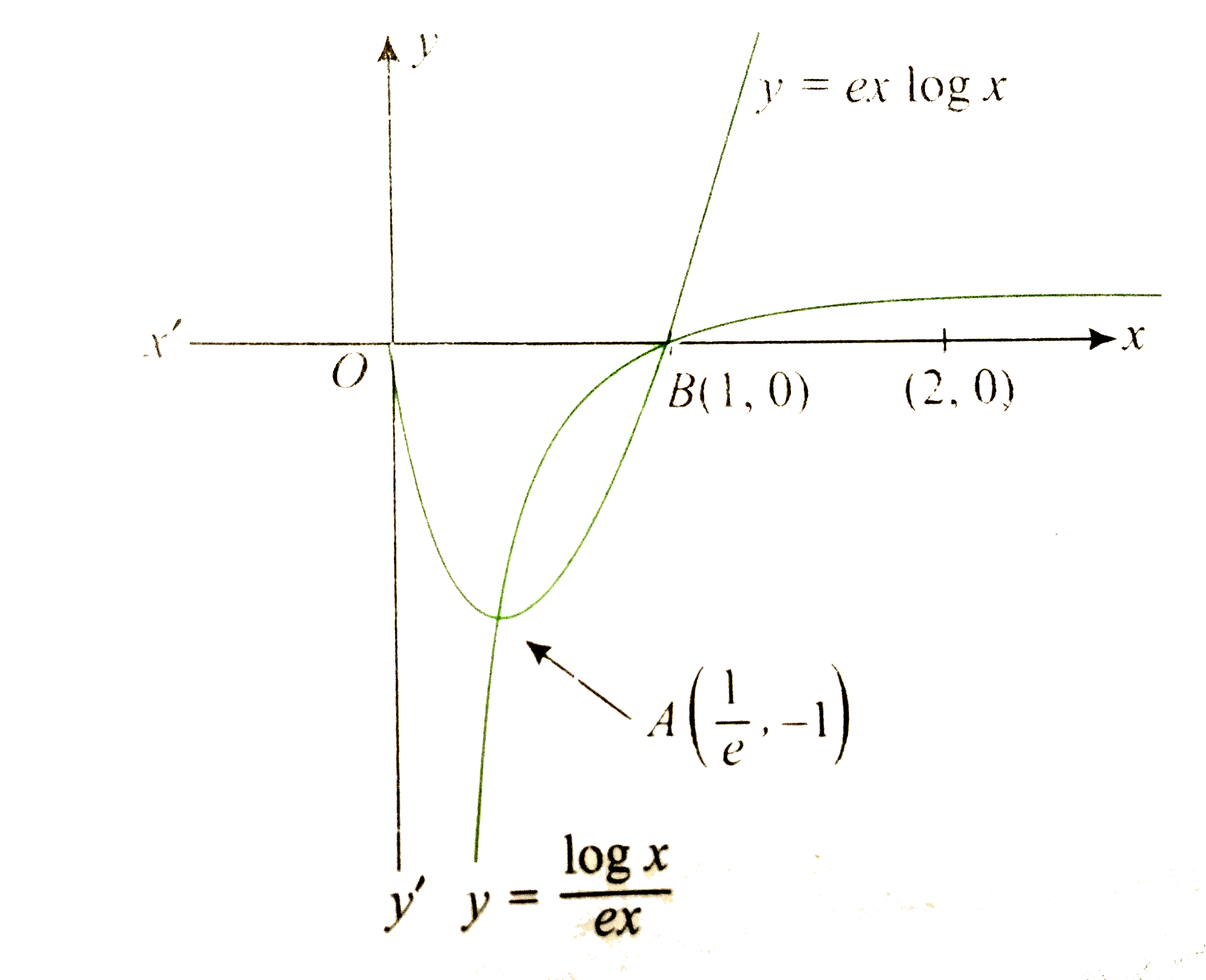
`therefore" "` Required area = Area of the shaded region
`=|int_(1//e)^(1)[ex log x -(log x)/(ex)]dx|`
`=|e[(x^(2))/(2) log x -(x^(2))/(4)]_(1//e)^(1)-(1)/(e)[((log x ))/(2)]_(1//e)^(1)|`
`=|e[(-(1)/(4))-(-(1)/(2e^(2))-(1)/(4e^(2)))]-(1)/(e)[0-(1)/(2)]|`
`|e[-(1)/(4)+(3)/(4e^(3))]+(1)/(2e)|`
`=|(5-e^(2))/(4e)|=(e^(2)-5)/(4e)` sq. units.