Home
Class 12
MATHS
Let An be the area bounded by the curve ...

Let `A_n` be the area bounded by the curve `y=(tanx)^n` and the lines `x=0,y=0,` and `x=pi/4dot` Prove that for `n >2,A_n+A_(n-2)=1/(n-1)` and deduce `1/(2n+2)

Text Solution

Verified by Experts

`"We have "A_(n)=int_(0)^(pi//4)(tan x)^(n) dx`

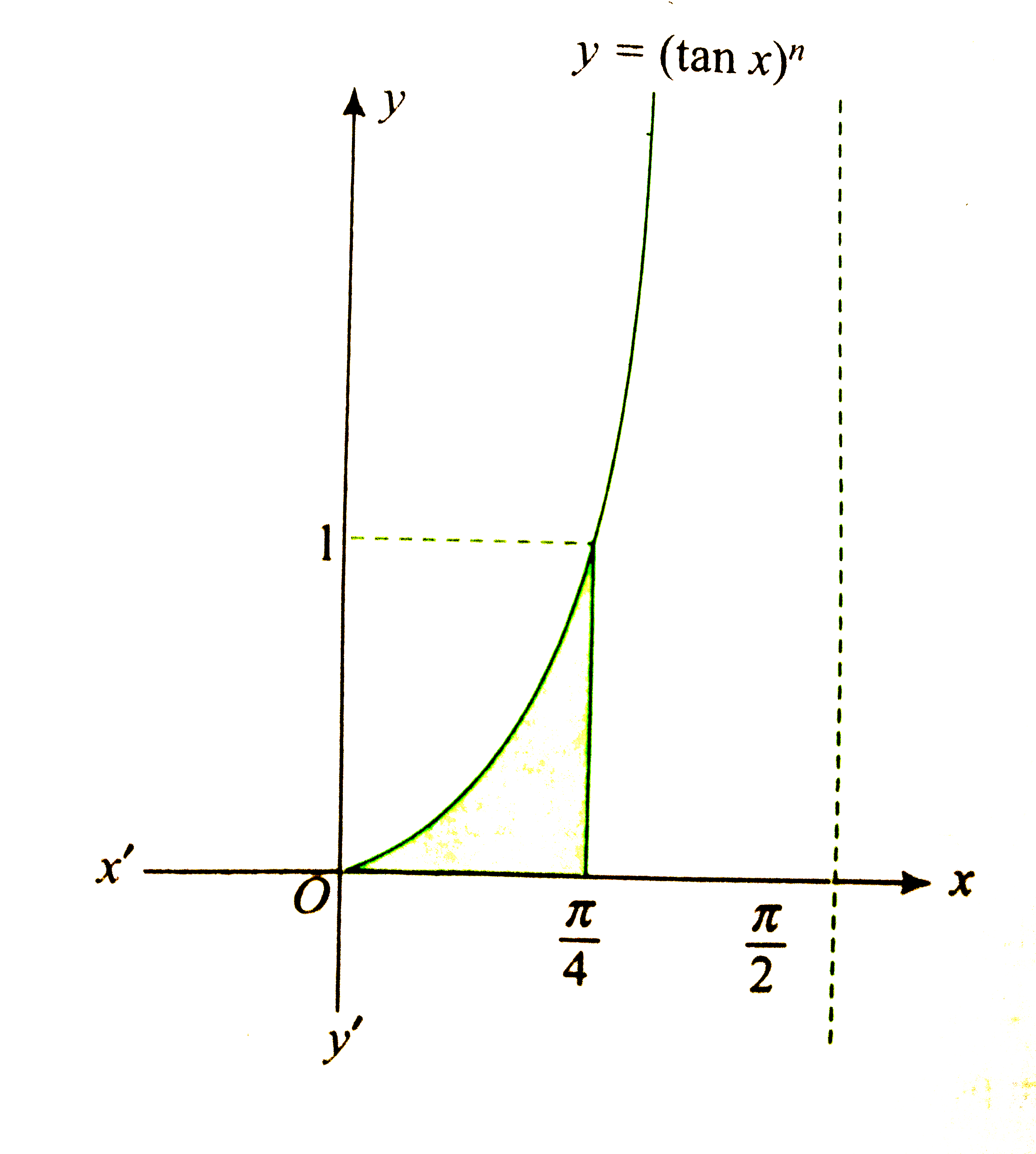
`"Since "0lt tna x lt 1," when "0 lt x lt pi//4,` we have
`0lt (tan x)^(n+1) lt (tan x)^(n)" for each "n in N`
`rArr" "int_(0)^(pi//4)(tan x)^(n+1) dx lt int_(0)^(pi//4) (tan x)^(n) dx`
`rArr" "A_(n+1)ltA_(n)`
`"Now, for "ngt2`,
`A_(n)+A_(n+2)=int_(0)^(pi//4)[(tan x)^(n)+(tan x)^(n+2)]dx`
`=int_(0)^(pi//4)(tan x)^(n)(1+ tan^(2)x) dx`
`=int_(0)^(pi//4)(tan x)^(n) (sec^(2)x) dx`
`=[(1)/((n+1))(tan x)^(n+1)]_(0)^(pi//4)`
`[because int [f(x)]^(n)f'(x)dx=([f(x)]^(n+1))/(n+1)]`
`=(1)/((n+1))(1-0)`
`"Since "A_(n+2)ltA_(n+1)ltA_(n),` we get
`A_(n)+A_(n+2)lt2A_(n)`
`rArr" "(1)/(n+1)lt2A_(n)rArr(1)/(2n+2)ltA_(n)" (1)"`
`"Also for "ngt2, A_(n)+A_(n)ltA_(n)+A_(n-2)=(1)/(n-1)`
`"or "2A_(n)lt(1)/(n-1)`
`"or "A_(n)lt(1)/(2n-2)" (2)"`
`"Combining (1) and (2), we get "(1)/(2n+2)ltA_(n)lt(1)/(2n-2).`
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE|Exercise Exercise 9.1|9 Videos

  • AREA

    CENGAGE|Exercise Exercise 9.2|14 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE|Exercise Question Bank|29 Videos

  • AREA UNDER CURVES

    CENGAGE|Exercise Question Bank|20 Videos

Similar Questions

Explore conceptually related problems

If A_n be the area bounded by the curve y=(tanx^n) ands the lines x=0,\ y=0,\ x=pi//4 Prove that for n > 2. , A_n+A_(n+2)=1/(n+1) and deduce 1/(2n+2)< A_(n) <1/(2n-2)

Let A_(n) be the area bounded by the curve y=x^(n)(n>=1) and the line x=0,y=0 and x=(1)/(2). If sum_(n=1)^(n)(2^(n)A_(n))/(n)=(1)/(3) then find the value of n .

If the area bounded by the curve y=cos^-1(cosx) and y=|x-pi| is pi^2/n , then n is equal to…

If A_(n) is the area bounded by y=(1-x^(2))^(n) and coordinate axes,n in N, then

If A_(n) is the area bounded by y=x and y=x^(n), n in N, then A_(2).A_(3)…A_(n)=

If A_(n) is the area bounded by y=x and y=x^(n),n in N, then A_(2)*A_(3)...A_(n)=(1)/(n(n+1)) (b) (1)/(2^(n)n(n+1))(1)/(2^(n-1)n(n+1)) (d) (1)/(2^(n-2)n(n+1))

Let {A_n} be a unique sequence of positive integers satisfying the following properties: A_1 = 1, A_2 = 2, A_4 = 12, and A_(n+1) . A_(n-1) = A_n^2 pm 1 for n = 2,3,4… then , A_7 is

A_1,A_(2) ....A_(n) are points on the line y=x lying in the positive quadrant such that OA_(n)=nOA_(n-1) .O being the origin.If OA_(1)=1 and the coordinates of A_n ,are (2520sqrt(2),2520sqrt(2)) ,then n=