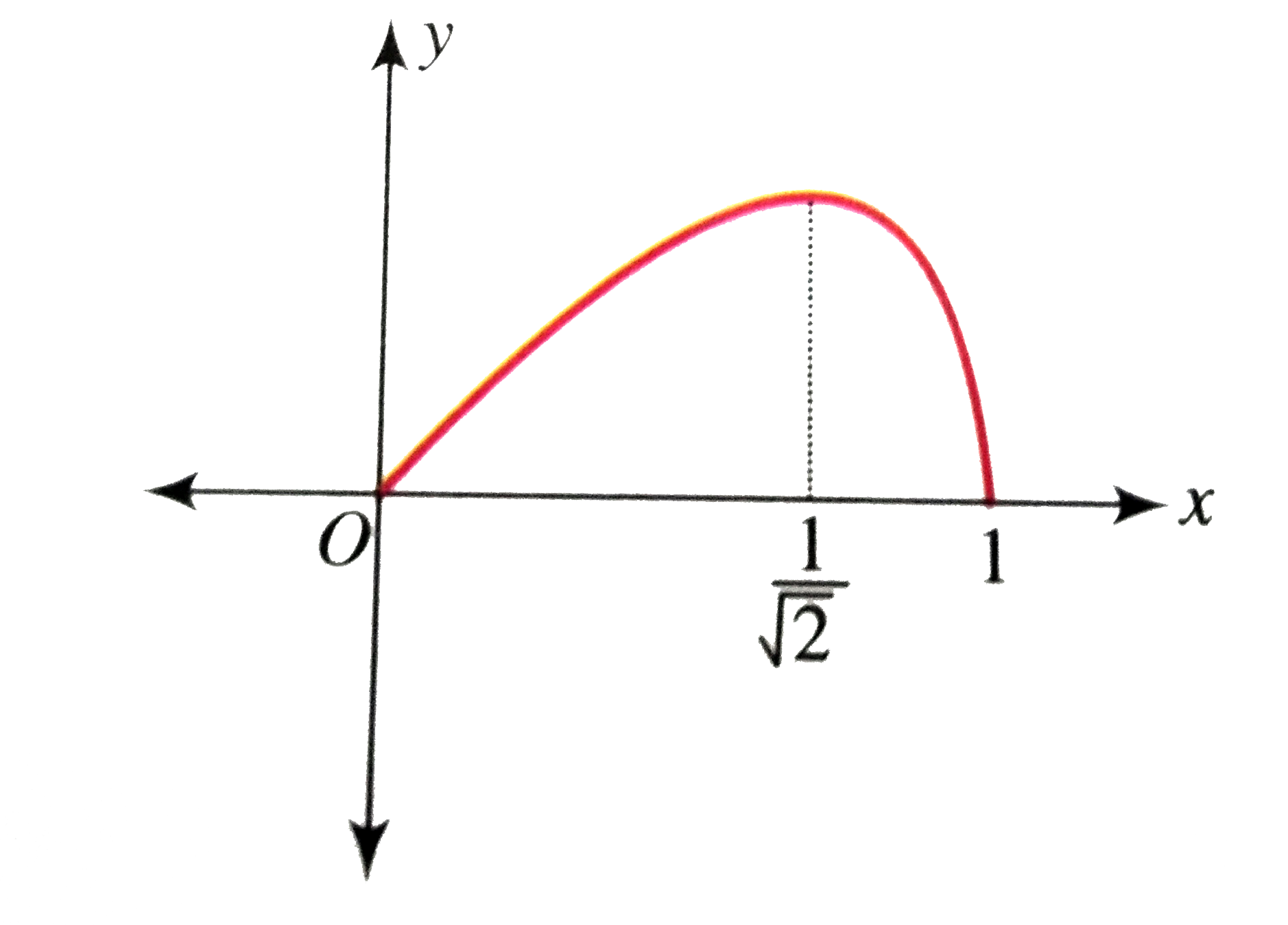
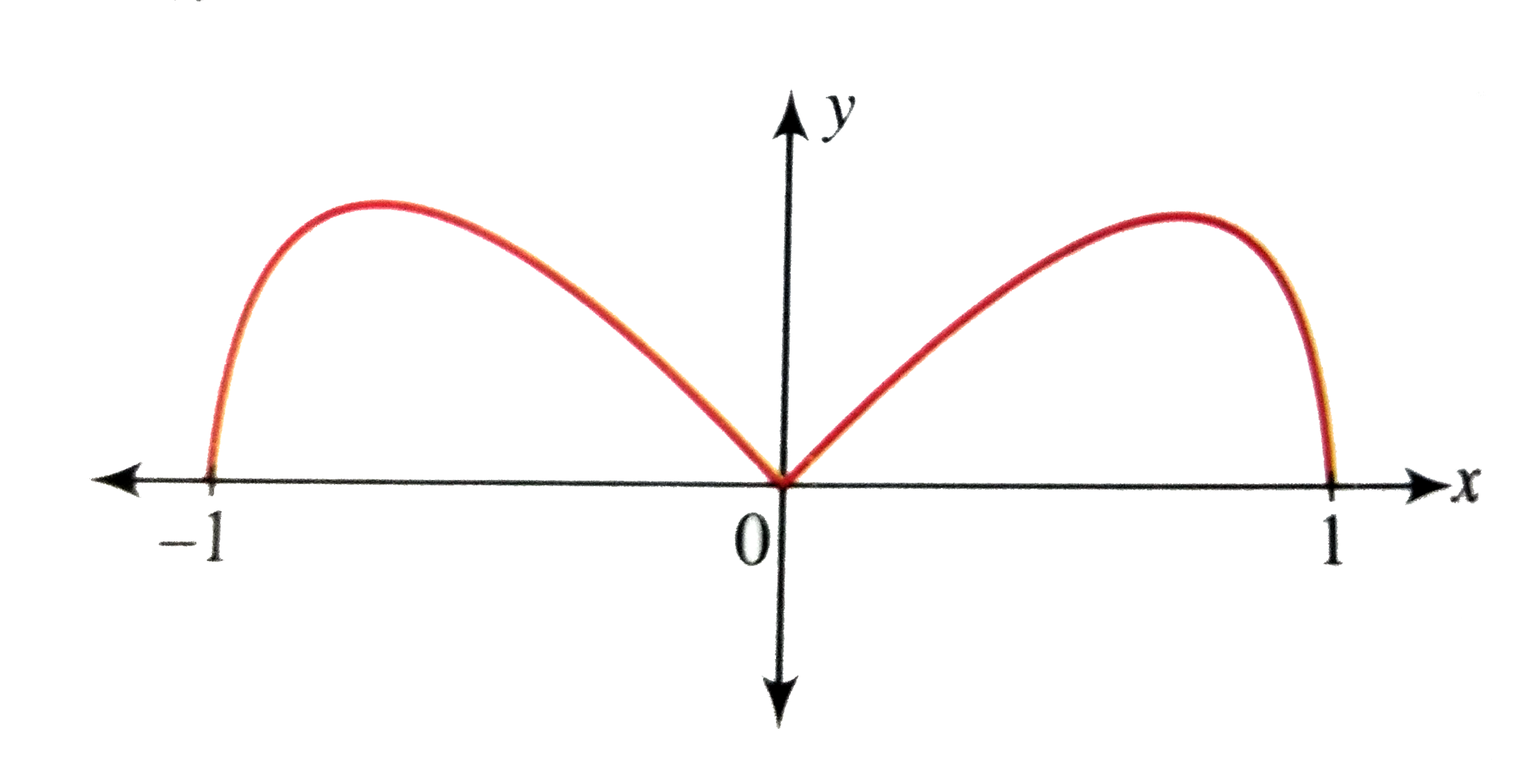
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-CURVE TRACING-Exercise
- Draw the graph of y=(sqrt(x^(2)+1)-sqrt(x^(2)-1))
Text Solution
|
- Draw the graph of y=sqrt(x)/(x-1)
Text Solution
|
- Draw the graph of the relation y=|x|sqrt(1-x^(2))
Text Solution
|
- Draw the graph of y=sqrt((x-1)/(1+x))
Text Solution
|
- Draw the graph of sqrt(|x|) + sqrt(|y|)=1
Text Solution
|
- Draw the graph of y=(3sqrt(x^(2)+1))/(x-1)
Text Solution
|
- Draw and discuss the graph of the function f(x) = e^(1//x)
Text Solution
|
- Draw the graph of y=1/(log(e)x)
Text Solution
|
- Draw the graph of y=1/(log(e)x)
Text Solution
|
- Draw the graph of f(x)=e^(-x^(2)). Discuss the concavity of the graph.
Text Solution
|
- Draw the graph of f(x) = e^(x)/(1+e^(x)). Also find the point of infle...
Text Solution
|
- Draw the graph of the function f(x)=x^(x)
Text Solution
|
- Draw the graph of y=x//"ln "x
Text Solution
|
- Draw the graph of y=(log(e)x)^(2)
Text Solution
|
- Draw the graph of y=log(e)(x^(2)-1)
Text Solution
|
- Draw and graph of f(x) = (4log(e)x)/(x^(2)). Also find the range.
Text Solution
|
- Draw the graph of the relation y^(2)=x^(5)(2-x)
Text Solution
|
- Draw the graph of f(x) = 2x+3x^(2//3) and discuss the type of non-diff...
Text Solution
|
- The function f(x)=x^(1/3)(x-1) has two inflection points has one poin...
Text Solution
|
- Draw the graph of y=(e^(x)-e^(-x))/(2).
Text Solution
|