A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GEOMETRY
PEARSON IIT JEE FOUNDATION|Exercise very Short answer Type Question|25 VideosGEOMETRY
PEARSON IIT JEE FOUNDATION|Exercise Short answer Type Question|29 VideosFORMULAS
PEARSON IIT JEE FOUNDATION|Exercise ASSESSMENT TESTS (Test 2)|8 VideosINDICES
PEARSON IIT JEE FOUNDATION|Exercise Test -2|12 Videos
Similar Questions
Explore conceptually related problems
PEARSON IIT JEE FOUNDATION-GEOMETRY -Test-2
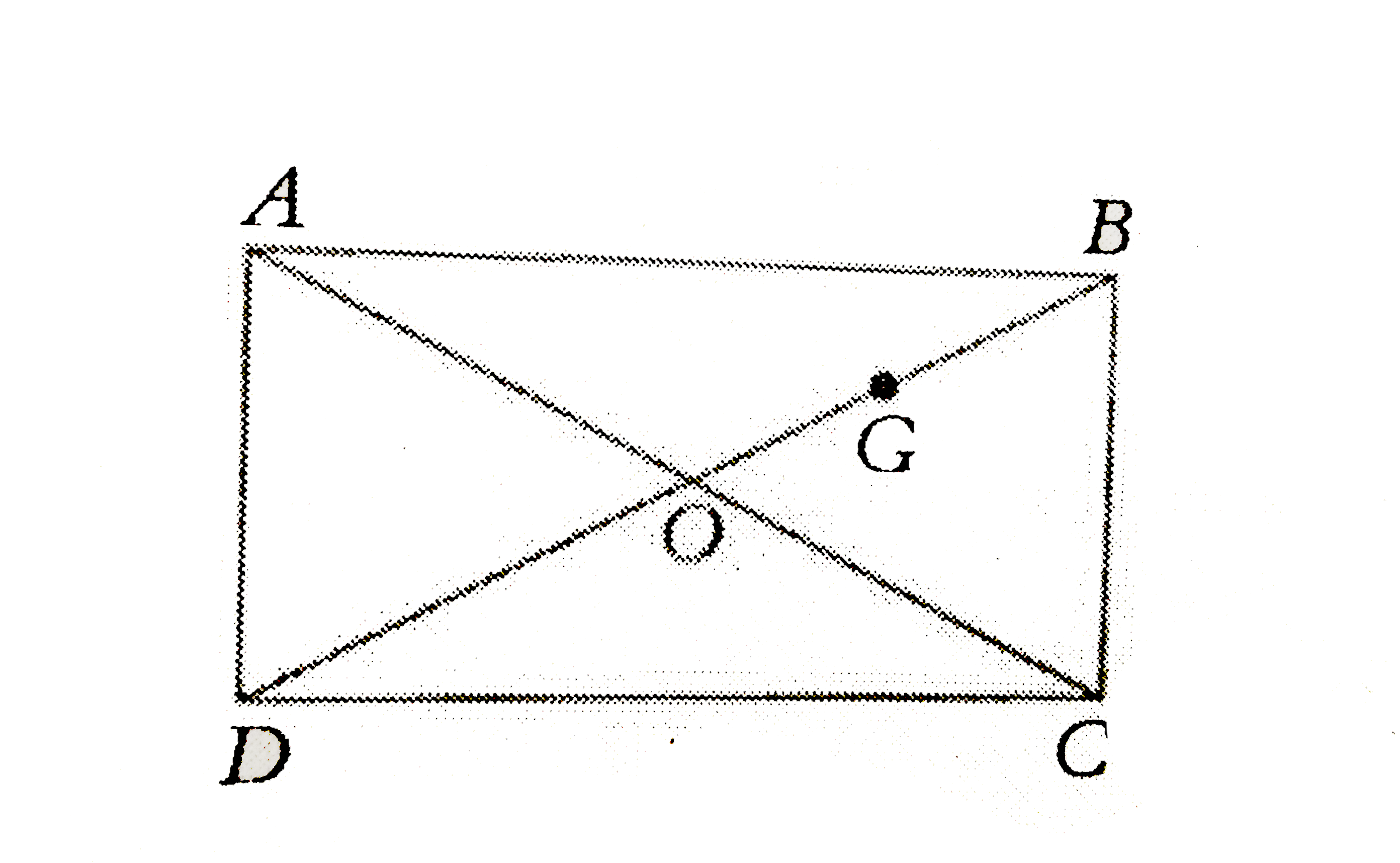
- In the figure, ABCD is a rectangle and G is the centroid of the triang...
Text Solution
|
- The measures of the angle of a triangle are in the ratio of 1:2:3. fin...
Text Solution
|
- The measure of the angle of a quadrilateral are 40^(@), 80^(@) and 10...
Text Solution
|
- Find the number of sides of a regular polygon, if the measure of each ...
Text Solution
|
- In a quadrilateral PQRS, bar(PQ)||bar(RS) and PR=QS. PQRS is a /an
Text Solution
|
- In the given figure, bar(AE) ||bar(CD), AB=BC, and AE=CD. If bar(AC) b...
Text Solution
|
- The measure of one of the angles of an isosceles triangle is 94^(@). W...
Text Solution
|
- In the given figure, if l||m, then what type of a triangle is ABC ?
Text Solution
|
- In the given figure, angleACB=60^(@), angleCAB=50^(@) and BC=BD. Find ...
Text Solution
|
- In the given figure, ABCD is a quadrilateral angleADB=60^(@), angleBAC...
Text Solution
|
- One angle of a parallelogram is thrice its adjacent angle. Which of th...
Text Solution
|
- Which of the following statement is true ?
Text Solution
|
- Match the following Column A and Column B
Text Solution
|