Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FULL MARKS-SAMPLE PAPER 3 (SOLVED)-PART- IV
- Explain in detail the construction and working of a Van de Graaff gene...
Text Solution
|
- Explain the equivalent resistance of a series and parallel resistor ne...
Text Solution
|
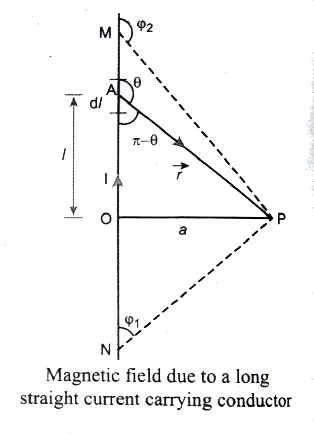
- Deduce the relation for the magnetic induction at a point due to an in...
Text Solution
|
- Show that the mutual inductance between a pair of coils is same (M(12)...
Text Solution
|
- Derive the equation for refraction at single spherical surface.
Text Solution
|
- What do you mean by electron emission ? Explain briefly various method...
Text Solution
|
- Discuss the spectral series of hydrogen atom.
Text Solution
|
- State and prove De Morgan's Frist and second theorems.
Text Solution
|
- What is modulation? Explain the types of modulation with necessary dia...
Text Solution
|
- Elaborate any two types of Robots with relevant examples.
Text Solution
|