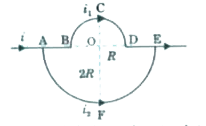
Text Solution
Verified by Experts
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT FILE (NCERT Textbook Exercises)|13 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT FILE (NCERT Additional Exercises)|15 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise Conceptual Questions|29 VideosMAGNETISM AND MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|16 VideosNUCLEI
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-MOVING CHARGES AND MAGNETISM-Tough & Tricky (PROBLEMS )
- A flat disc of radius R charged uniformly on its surface at a surface ...
Text Solution
|
- A wire of uniform cross section is used to make the given system. The ...
Text Solution
|
- A uniform magnetic field is applied in a circular region of radius R a...
Text Solution
|
- A uniform electric field and a uniform magnetic field are acting along...
Text Solution
|
- A long wire carrying a current i is bent to form a plane angle theta. ...
Text Solution
|
- A capacitor of capacitance 100 mu F is connected to a battery of 20 vo...
Text Solution
|
- A circular loop of radius R, carries current. At what distance from th...
Text Solution
|
- A uniformly charged ring of radius R is rotated about its axis with co...
Text Solution
|
- The path of a charged particle moving in a uniform steady magnetic fie...
Text Solution
|
- Let there be one sheet of infinite length and breadth is shown in the ...
Text Solution
|
- Two metal sheets of infinite width carrying current K per unit width, ...
Text Solution
|
- A long, straight wire carries a current i. Let B1 be the magnetic fiel...
Text Solution
|
- Two equal point charges q are moving parallel to each other with the s...
Text Solution
|
- There is one long solenoid with turns per unit length. The radius of t...
Text Solution
|
- A metallic sphere rotates with angular speed and its surface charge de...
Text Solution
|