विस्थापन धारा- एम्पेयर के परिपथीय नियम के अनुसार, " किसी बंद लूप के लिए चुम्बकीय क्षेत्र `vecB` का रेखीय समाकल उस लूप द्वारा घेरे गए क्षेत्रफल से होकर प्रवाहित कुल धारा `i` का `mu_(0)` गुना होता है |
`ointvecB*dvec1=mu_(0)i(t)`
जहाँ `mu_(0)` निर्वात की चुम्बकशीलता है|
आवश्यकता का कारण-वैद्युत धारा के चुम्बकीय प्रभाव तथा वैद्युतचुम्बकीय प्रेरण जेसी घटनाओं से ज्ञात हुई है की वैद्युत धारा चुम्बकीय क्षेत्र उत्पन्न करती है तथा समय के साथ परिवर्ती चुम्बकीय क्षेत्र भी चुम्बकीय क्षेत्र उत्पन्न करता है| मैक्सवेल ने समय के साथ परिवर्ती धारा से सम्बन्ध संधारित्र के बाहर किसी बिंदु पर चुम्बकीय क्षेत्र ज्ञात करने के लिए एम्पेयर का प्रिपथीय नियम प्रयुक्त करते समय पाया की इसमे एक विसंगति है जिए दूर करने के लिए उन्होंने एक अतिरिक्त धारा के अस्तित्व का सुझाव दिया जिसे उन्होंने विस्थापन धारा का नाम दिया |
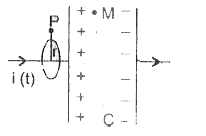
एम्पेयर- मैक्सवेल परिपथीय समीकरण- माना एक समांतर प्लेट संधारित्र `C` ऐसे वैद्युत परिपथ में जुदा है जिसमे समय के साथ परिवर्ती धारा `i(t)` प्रवाहित हो रही है |
समान्तर प्लेट संधारित्र के बाहर किसी बिंदु P पर चुम्बकीय क्षेत्र ज्ञात करने के लिए, धारावाही चालाक तार को केंद्र मानकर r त्रिज्या का एक वृत्ताकार लूप लेते है, जिसका तल तार के लम्बवत है, बिंदु P जिसकी परिधि पर स्थित है | (चित्र)
एम्पेयर के परिपथीय नियम के अनुसार
`ointvecB*dvec1=ointBdlcos0^(@)=mu_(0)i(t)`
अथवा `Bointdl=mu_(0)i(t)`
अथवा `B(2pir)=mu_(0)i(t)` `(becauseointdl=2pir)`
एम्पेयर के परिपथीय नियम से,
`ointvecB*dvec1=B*2pir=0`
अंत: बिंदु P पर चुम्बकीय क्षेत्र B=0
यदि समान्तर प्लेट संधारित्र की प्लेटो का क्षेत्रफल A, उन पर आवेश q तथा आवेश का पृष्ठ घनत्व `sigma` हो तब उसकी प्लेटो के बिच
वैद्युत क्षेत्र `E=(sigma)/(epsi_(0))=(q)/(epsi_(0)A)" "(becausesigma=(q)/(A))`
गॉस की प्रमेय के अनुसार, प्लेटो के बिच समतल सतह (जहाँ वैद्युत क्षेत्र लम्बवत है) से गुजरने वाला वैद्युत फ्लक्स
`phi_(E)=E*A=(q)/(epsi_(0)A)*A=(q)/(epsi_(0))`
अथवा `q=phi_(E)epsi_(0)` . . . (2)
यदि संधारित्र की प्लेटो पर आवेश q समय के साथ परिवर्ती हो तब इसके सांगत एक धारा सम्बन्ध होगी जिसका मान
`i=(dq)/(dt)=(d)/(dt)(epsi_(0)phi_(E))=epsi_(0)((dphi_(E))/(dt))`
अंत: इसे मैक्सवेल की विस्थापन धारा कहते है| इसका मात्रक एम्पेयर है| किसी भी सतह जिसकी परिमिति बंद लूप है, में प्रवाहित कुल धारा `i`, चालन धारा `i_(c)` व् विश्थापन धारा `i_(d)` के योग के बराबर होती है |
अर्थात `i=i_(c)+i_(d)`
इसका अर्थ है कि संधारित्र की प्लेटो के बाहर चालन धरा, `i_(c)=i` तथा विस्थापन धारा `i_(d)=0` होती है| दूसरी ओर संधारित्र के भीतर चालन धारा `i_(c)=0` तथा विस्थापन धारा `i_(d)=i` होती है |
अंत: व्यापक रूप में एम्पेयर का परिपथीय नियम
`ointvecB*dvec1=mu_(0)(i_(c)+i_(d))=mu_(0)i_(c)+mu_(0)i_(d)`
`=mu_(0)i_(c)+mu_(0)epsi_(0)(dphi_(E))/(dt)`
इसे एम्पेयर-मैक्सवेल नियम कहते है |
