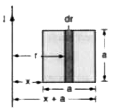
(a) वर्गाकार लूप पर dr चौड़ाई की एक छोटी पट्टी लें जो सीधी तार से r दूरी पर है।
पट्टी का क्षेत्रफल `dA=a dr`
इस पट्टी पर चुम्बकीय क्षेत्र `B=(mu_(0)I)/(2pi r)`
(`vecB`, पृष्ठ के तल में अन्दर की ओर है)
पट्टी से जुड़ा चुम्बकीय फ्लक्स `dphi_(B)=B(dA)`
`=(mu_(0)I)/(2pi r)(a dr)`
वर्ग से सम्बद्ध कुल चुम्बकीय फ्लक्स
`phi_(B)=(mu_(0)Ia)/(2pi) int_(x)^(x+a) (1)/(r )dr`
`=(mu_(0)Ia)/(2pi)|"In r"|_(x)^(x+a)=(mu_(0)Ia)/(2pi)["In"(x+a)-"In"x]`
`=(mu_(0)Ia)/(2pi)"In"(1+(a)/(x))`
क्योंकि `phi_(B)=MI`, इसलिए `M=(phi_(B))/(I)=(mu_(0)a)/(2pi)"In"(1+(a)/(x))`
(b) `epsilon= -(dphi_(B))/(dt)= -((dphi_(B))/(dx)) ((dx)/(dt))= -v ((dphi_(B))/(dx))" "` (क्योंकि `(dx)/(dt)=v`)
`=-v (d)/(dx)[(mu_(0)Ia)/(2pi)"In"(1+(a)/(x))]`
`= -v((mu_(0)Ia)/(2pi)) (1)/((1+(a)/(x))) ((-a)/(x^(2)))`
`=(mu_(0)I a^(2)v)/(2pi x(x+a))`
यहाँ `I=50A, a=0.1m, v=10m//s` और `x=0.2m`
इस प्रकार
`epsilon=((4pi xx 10^(-7))(50)(0.1)^(2)(10))/(2pi (0.2)(0.2+0.1))V=1.7xx10^(-5)V`