शारिता-किसी चालक के विभव में ईकाई वृद्धि करने के लिए आवश्यक आवेश को र की विद्युत धारिता कहते हैं । दूसरे शब्दों में, धारिता विद्युत् आवेश एवं विभव के अनुपात को कहते हैं।
Sl मात्रक = फेराड `(F) = CV^(-1)`
समांतर प्लेट संधारितत्र में स्थिर वैद्युत उर्जा-माना कि संधारित्र की धारिता C है तथा उस क्षण उस पर कोई आवेश नहीं है । संधारित्र को बैटरी से जोड़ने पर वह V विभव तक आवेशित होता है । अगर संधारित्र पर q आवेश जमा होता है, तब `q= CV`
यदि संधारित्र में अतिरिक्त आवेश dq स्थानांतरित किया जाता है तो इसके लिए किया गया कार्य संधारित्र विद्युत उर्जा के रूप में संचित रहता है
`dv = dw = Vdq = (q)/(C) dq`
संधारित्र को `q=0` से `q=theta` तक आवेशन `theta` तक आवेशन में स्थितिज उर्जा में कुल वृद्धि संधारित्र में कुल संचित उर्जा के बराबर होती है ।
`:.U=intdu=int_(0)^(q)(q)/(c)int_(0)^(q)qdq=(1)/(2c)[q^(2)]_(0)^(q)=(1)/(2c)[q^(2)-0]`
`:.V=(1)/(c)[(theta^(2))/(2)]`
Q=cV
`:.V=(1)/(C).(C^(2)v^(2))/(2)=(1)/(2)cV^(2), V=(1)/(2)cV`
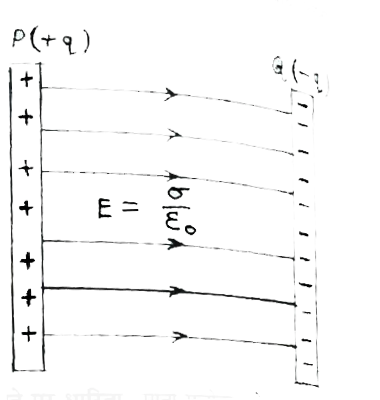
अथवा समान्तर प्लेट वाले संधारित्र की धारिता का व्यंजक-माना कि संधारित्र को दानों व्य दूरी है जैसा कि चित्र में दिखाया गया है । प्लेट P का धनात्मक आवेश (+q) .ऋणात्मक आवेश दिया जाता है । माना कि प्लट P तथा Qका पृष्ठ आवश था `(- q)` है । प्लेटों के मध्य विद्यत क्षेत्र इस प्रकार व्यक्त किया जाता है ।
`:.E=(sigma)/(epsilon_(0))`
जहाँ `epsilon_(0)` = निरपेक्ष विद्युतशीलता है क्योकि प्लटा के मध्य माध्यम के बीच विभवांतर । है तब V = Ed
`V=(sigma)/(epsilon_(0))d`
`sigma=(q)/(A) :.V=(q)/(epsilon_(0))(d)/(A)...(ii)`
`C=(q)/(V)`
`C=(qepsilon_(0)A)/(qd)=(epsilon_(0)A)/(d)`
`C=(epsilon_(0)A)/(d)`Ans.
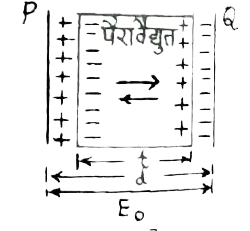
संधारित्र के समान्तर प्लेट के बीच माध्यम रखने पर धारिता-माना प्रत्येक प्ले तथा क्षेत्रफल क्रमश: t तथा A है तथा दोनों प्लेटों के मध्य की दूरी d है। माध्यम पर पर बराबर तथा विपरित आवेश उपस्थित हो जाता है । इन प्रेरित आवेश के कारणरित आवेश के कारण प्रेरित विद्युत क्षेत्र `(vecE_(p))`में उत्पन्न हो जाता है जो कि आरोपित क्षेत्र `(vecE_(0))`की दिशा के विपरीत दिशा में होता है जैसा कि निम्न चित्र में दिखाया गया है।
निर्वात है । यदि प्लाअत: विद्युत क्षेत्र का पराविद्युत मे समानीत मान `E = E_(0)-E_(p)`
अब .t. मोटाई के पराविद्युत में विद्युत क्षेत्र `E = E_(0)-E_(p)` तथा `(d-t)` मोटाई के क्षेत्र में विद्युत क्षेत्र `E_(0)` है ।
संधारित्र की दोनों प्लेटों के मध्य विभांतर निम्नवत् व्यक्त किया जाता है ।
`V= E_(0) (d -t) + Et` चूँकि `(E_(0))/(E)=K` या `E=(E_(0))/(K)`
`:. V = E_(0) (d -t) + (E_(0))/(K)t`
`V= E_(0)(d-t) (E_(0))/(K) t`
`V=E_(0)[(d-t)+(t)/(K)]....(i)`
हम जानते हैं `E_(0) =(sigma)/(epsilon_(0))=(q)/(epsilon_(0)`
:.. समी. () को निम्न प्रकार लिख सकते हैं ।`V=(q)/(Aepsilon_(0))[(d-t)+(t)/(K)]...(ii)`
अब संधारित्र की धारिता
`C=(q)/(nu)=(qAepsilon_(0))/(q[(d-t)+(t)/(K)]]`
`C=(qepsilon_(0)A)/((d-t)+(t)/(K))`
`C=(Aepsilon_(0))/(d[(1-(t)/(d))+(t)/(dK)]]...(iii)`
कि हम जानते हैं `C_(0) = (epsilon_(0)A)/(d)`
जहाँ ` epsilon_(0)`प्लेटों के बीच प्लेटों के बीच निर्वात संधारित्र की धारिता ।
(iii) को (iv) से भाग देने पर
`(C)/(C_(0))=(1)/([(1-(t)/(d))(t)/(dK)]]=(1)/([1-(t)/(d)(1-(1)/(K))]]`
`C=(C_(0))/([1-(t)/(d)(1-(1)/(K))]]....(v)`
समी. (v) से स्पष्ट है कि `CgtC_(0)`
आत किसी समान्तर प्लेट संधारित्र प्लेटों के मध्य पराविद्युत रखने पर इसी धारिता में वृद्धि हो जाती है।