माना ABC किसी प्रिज्म का मुख्य काट है, जिसका अपवर्तन कोण A है । जैसा कि निम्न चित्र में दर्शाया गया है ।
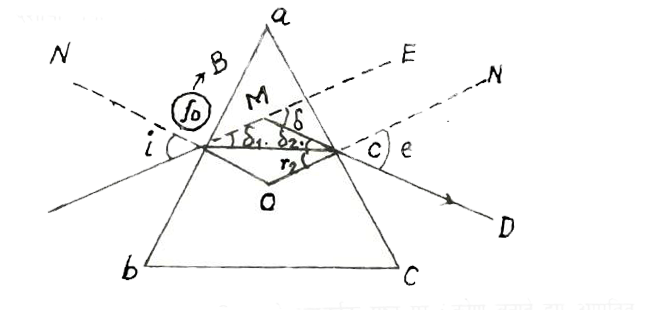
माना एक प्रकाश किरण A B इस प्रिज्म के अपवर्तक पृष्ठ पर । कोण बनाते हुए आपतित लाता है । बिन्दु B पर अपवर्तन के पश्चात् यह प्रकाश किरण अभिलम्ब NO की ओर मुड़ जाती तथा BC के अदिश गति करती है । इस अपवर्तित किरण BC का बिन्दु C पर पुन: आपतन है और यह अभिलम्ब N.0 से दर चली जाती है तथा CD के अनुदिश गति करती है। .करण अभिलम्ब के साथ कोण `(/_e)` बनाती है । अगर CD को आगे तरफ बढ़ाया जाए सतत किरण को M बिंद पर काटती है। आपतित किरण तथा CD के बीच का कोण `delta` मान लत हैं, जो कि विचलन कोण कहलाता है । चित्र से स्पष्ट है-`/_FRC = /_ABN-/_CBO`
`delta_(1)=i-r_(1)` तथा `delta_(2) = e-r_(2)`
:. कुल विचलन कोण, `delta=delta_(1)+delta_(2)`, या `delta=i-r_(1)+e-r_(2)`
चतुभुज aBOC से. `delta= (i+e)-(r_(1)+r_(2)`
` /_A+/_aBO+/_BOC+/_OCA = 360^(@)`
`/_ABO = /_OCa= 90^(@)`
`/_a+90^(@)+/_BOC+90^(@) = 360^(@)`
`/_A+/_BOC = 180^(@)`....(ii)
`/_\BOC` से, `/_r_(1) +/_BOLI +/_r_(2)=180^(@)` समी
(ii) और (iii) से तुलना करने पर,
`/_A+/_BOC =/_r_(1) +/_BOC+/_r_(2)`
`A = r_(1)+r_(2)`
समी. (i) और (ii) से, `delta = i+e -A`
`delta + A = i+e`
यदि `delta= deltam i =e` ( तथा `r_(1)=r_(2)=r` (प्रिज्म न्यूनतम विचलन स्थिति
समो. (v) से. `deltam+ A =2i`या `i =(A+deltam)/(2)....(iv)`
समी. (iv))से, `2r = A` या `r = A//2`.....(vii)
स्नेल के नियम से,`n=(sini)/(sinr)`
समी. (vi) और (vii)`sin((A+deltam)/(2))/(sin(A)/(2))`सिद्ध हुआ ।
अथवा, समतुल्य लेंस-यदि दो या दो से अधिक समीक्षीय लेंसों के युग्म के बदले एक ऐसा लेंस लिया जाए, जिसे लेंस युग्म के अक्ष पर उपयुक्त स्थान पर रखने से किसी वस्तु का प्रतिबिम्ब उसी स्थान पर तथा उतने ही आवर्धन का बने, जैसा कि लेंस युक्त द्वारा होता है, तो उस अकेले लेंस को लेंस-युग्म का समतुल्य लेंस कहा जाता है ।
समतुल्य फोकस दूरी का व्यंजक-माना कि दो लेंस `L_(1)`, तथा `_(2)` जिनकी फोकस दूरी `f_(1)` तथा `f_(2)`, है एक-दूसरे के साथ स्पर्श करते हुए रखे हुए हैं। माना कि मुख्य अक्ष पर O एक बिन्दु रखा हआ है।
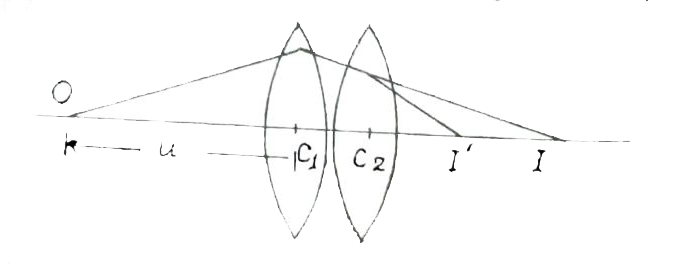
इस बिन्दु बिंब का दो पदों में प्रतिबिंब | बनता है ।
प्रथम पद-इस पद में `L_(1)` बिंदु बिंब का प्रतिबिम्ब I बनता है ।
यदि `C_(1)O=u` तथा `C_(1)I = nu`
`(1)/(u)+(1)/(nu)=(10/(f_(1))`
दसरा पद-इस पद में `C_(2)` प्रतिबिम्बl l बनाता है जो काल्पनिक है । चौक दानों लंस पतले हैं।
`C_(2)I=C_(1)I=+V`
`C_(2)I=V`
`C_(2)I=V-(1)/(V))+(10/(V)=(1)/(f)`
समी. (1) तथा (ii) को जोड़न पर,
`-(1)/(u)+(1)/(V)-(1)/(V)+(1)/(v)=(1)/(f_(1)+(1)/(f_(2))`
`-(1)/(u)+(1)/(V)=(1)/(f_(2)) …(iii)`
कल लेंस जिसकी फोकस दूरी f fहो O बिंदु का प्रतिबिंब I बनाए, तो
`_(1)/(u)+(1)/(f)=(1)/(f)`
समी. (iii) एवं (iv) से,
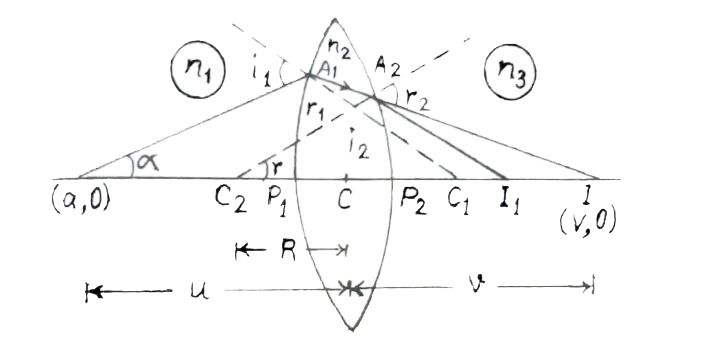
उपरोक्त चित्र से माना सतह X PY के द्वारा बिंदु 0 का प्रतिबिंब I बनाता है
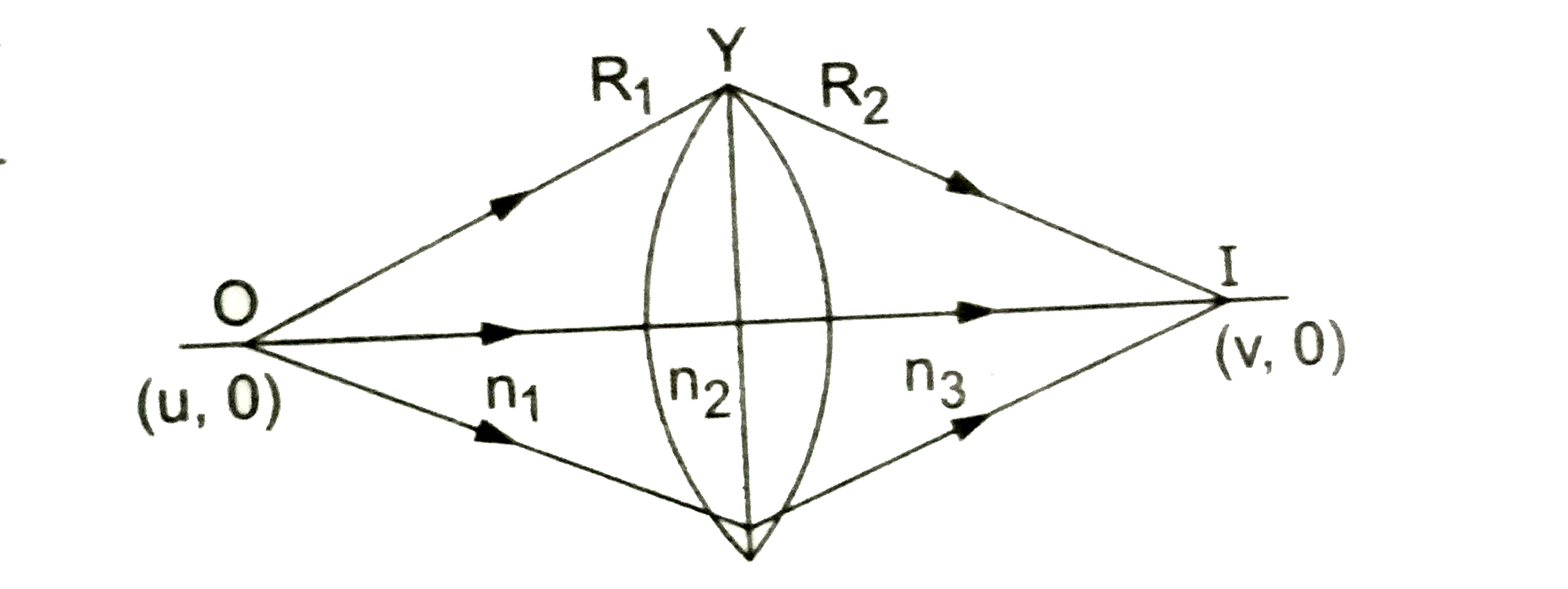
`(n_(1))/(P_(1)O)+(n_(2))/(P_(1)I)=(n_(2)-n_(1))/(P_(1)C_(1))`
अब `P_(1)O~~ CO, PL ~~ Cl` तथा `P_(1)C_(1) = C C_(1)` (चूँकि लेंस पतला है)
अतः समी. (i) इस प्रकार लिखा जा सकता है ।
`(n_(1))/(CO)+(n_(2))/(CI)=(n_(2)-n_(1))/(C C_(1)).....(ii)`
माना कि अब अपवर्तन XPY से हो रहा है तथा बिन्दु 1, पर वास्तविक प्रतिबिंब बना अतः`-(n_(2))/(P_(1)I)+(n_(3))/(P_(2)I_(1))=(mu_(2)-mu_(3))/(P_(2)C_(2))`
.चूँकि लैंस पतला है
अत: `P_(2)I ~~ C_(1). P_(2)i_(1) ~~ CI_(1))` तथा `P_(2)C_(2 )~~ C C_(2)`
समो. (iii) से,`-(n_(2))/(CI)+(n_(3))/(CI_(1))=(n_(2)-n_(3))/(C C_(2))....(iv)`
सभी. (ii) और (iv) को जोड़ने पर `(n_(1))/(Co)+(n_(2))/(CI)-(n_(2))/(CI)+(n_(3))/(CI_(1))=(n_(2)-n_(1))/(C C_(1))+(n_(2)-n_(1))/(C C_(2))`
`(n_(1))/(CO)+(n_(3))/(CI_(1))=(n_(2)-n_(1))/(C C_(1))=(n_(3)-n_(2))/(C C_(2))...(v)`
`:.CO=-u,CI_(1)=+R_(1),C C_(2)=-R_(2)`
`:.(n_(3))/(V)-(n_(1))/(u)=(n_(2)-n_(1))/(R_(1))+(n_(3)-n_(3))/(R_(2))`Proved