जब कुण्डली के निकट उत्तरी ध्रुव को लाया जाता है तब कुण्डली में का (counter clock-wise) दिशा में धारा प्रवाहित होती है
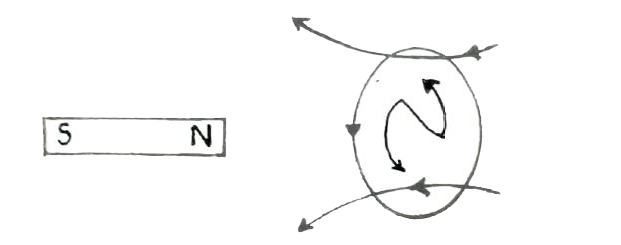
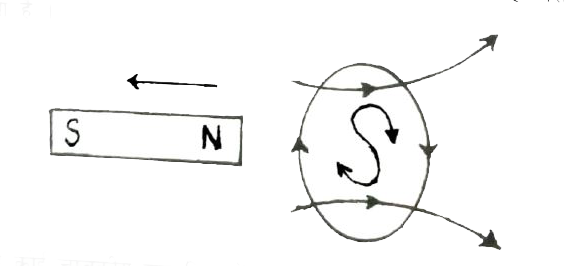
दक्षिण हस्त पेच के नियमानुसार यह प्रेरित धारा एक चुम्बकीय क्षेत्र उत्पन्न करती है, जो छड़ चुम्बक के चुम्बकीय क्षेत्र का विरोध करती है अर्थात् कुण्डली उत्तरी ध्रुव के रूप में व्यवहार करता है. जैसा कि उपरोक्त चित्र में दर्शाया गया है । इसी तरह जब छड़ चुम्बक उत्तरीध्रव पाश से दूर हटाया जाता है तब कुण्डली दक्षिणी ध्रुव की तरह व्यवहार करता है जैसा कि निम्न चित्र में दर्शाया गया है।
(ii) माना काई चुम्बकीय छड़ चित्र में दर्शाये गए अनसार किसी समरूप चुम्बकीय क्षत्र में स्थित है तो चुम्बक के उत्तरी तथा दक्षिणी ध्रव समान तथा विपरित बल अनुभव करत
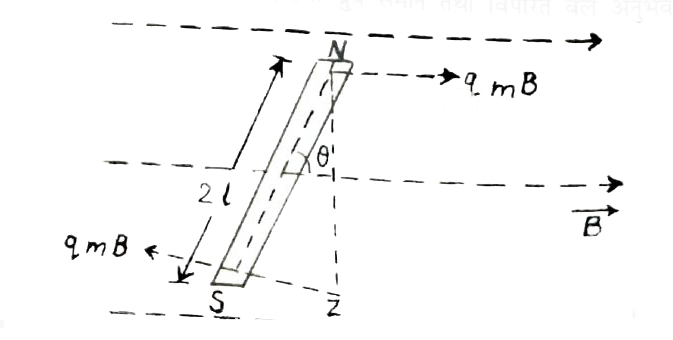
की लम्बाई, प्रत्येक ध्रुव की ध्रुव सामर्थ्य, चुम्बकीय क्षेत्र की सामर्थ्य तथा `vecB` गया कोण क्रमश: `21, q_(m) ,B` तथा `theta` है ।
मना चुम्बक की लम्बाई के सापेक्ष बनाया गया कोण व पर कार्यरत बल `q_(m)B` जा `vecB` के अनुदिश है तथा दक्षिणी ध्रुव पर कार्यरत बल उत्तरी ध्रुव पर कार्यरत बल ।
के विपरित है । ये बल एक युग्म का निर्माण करते हैं, जिसकी प्रवृत्ति चुम्बक को
`q_(m)B` जो `vecB` के विपरित है।
`vecB`की दिशा में घमाले में घमाने की होती है, इस प्रकार चुम्बकीय बल आघूर्ण अनुभव होता है । " अत: छड़ पर कार्यरत बल आघूर्ण
`tau=` बल `xx` बेलों के मध्य लम्बवत् दूरी `= q_(m)BxxZN ==mB(SN sin theta)`
`=q_(m) B (2l sintheta). = (q_(m)Xx2l)Bsin theta`
या `tau= MBsintheta`
सदिश रूप में`tau= vecMxx vecB` Ans
सबकीय क्षेत्र में चुम्बक को स्वेच्छ रूप से घुमाने पर किए गए कार्य-यदि द्विध्रुव कोण पर घूमाने किया गया कार्य `= domega = tuedtheta`
समी. (i) से, `domega = taudtheta = MB sin theta`
`theta से theta_(2)` तक घुमाने में कुल कार्य
`W=int_(theta_(1))^(theta_(2))Msind theta=Mbint_(theta_(1))^(theta_(2))sinthetadtheta`
`W=MB[-cos]_(theta_(1))^(theta_(2))=-MB[costheta_(2)-cos_(1)]`
`theta_(1)=90`
`theta_(2)=theta`
`w=-MB[costheta-costheta] w=-MBcostheta`
(i) If`theta = 0, W = - MB`
(ii) If `theta = 90^(@)W = 0`
(iii) If `theta 180^(@) W=MB`
अथवा, (i) जैसा कि हम जानते हैं
आवर्तकाल `(T)=(2pim)/(B_(2))=(2xx3.14xx9.1xx10^(-31))/(4xx1.6xx10^(-19))`
`=(3.14xx9.1xx10^(-12))/(3.2)=9xx10^(-2)S`
`T=9xx10^(2)S`
(ii) (क) जब दण्ड चुम्बक बराबर आकार के हो-`(M_(1))/(M_(2))=(T_(2)^(2))/(T_(1)^(2)`
(ख) दण्ड चुम्बक बराबर साईज के नहीं `(m_(1))/(M_(2))=(T_(2)^(2)+T_(1)^(2))/(T_(1)^(2)-T_(1)^(2))`


