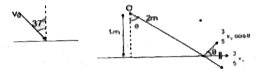
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COLLISION
FIITJEE|Exercise Exercise|20 VideosCOLLISION
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)|2 VideosCOLLISION
FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE) NUMERICAL BASED QUESTIONS|3 VideosAC CIRCUITS
FIITJEE|Exercise ASSERTION REASONING TYPE|1 VideosCURRENT ELECTRICITY
FIITJEE|Exercise Comprehension -4|3 Videos
Similar Questions
Explore conceptually related problems