Home
Class 12
PHYSICS
A block of mass m = 10 kg is pulled by a...

A block of mass m = 10 kg is pulled by a force F = 100 N at an angle `theta=30^(@)` with the horizontal along a smooth horizontal surface. What is the acceleration of the block? `(g = 10m//s^(2))`

Text Solution

Verified by Experts


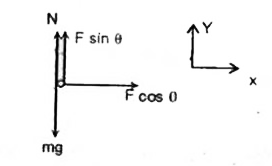
The F.B.D. of the block shows the force components.
Along X-axis, let let the acceleration of the block be .a.
`rArr F cos theta= m a " " ...(1)`
`rArr a=(F cos theta)/(m) " " ...(2)`
`=(100cos30^(@))/(10)=(100sqrt(3))/(2xx10)=5sqrt(3) m//s^(2)`
`therefore ` The acceleration of the block is `5sqrt(3)m//s^(2)` directed towards right. Since `F sin theta lt mg` & the surface is rigid, the block remains in equilibrium along Y-axis.
Promotional Banner

Topper's Solved these Questions

  • LAWS OF MOTION

    FIITJEE|Exercise SOLVED PROBLEMS (SUBJECTIVE)|11 Videos

  • LAWS OF MOTION

    FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE)|17 Videos

  • KINEMATICS

    FIITJEE|Exercise NUMERICAL BASED QUESTIONS DECIMAL TYPE|5 Videos

  • MAGNETIC

    FIITJEE|Exercise Numerical Based Type|2 Videos

Similar Questions

Explore conceptually related problems

A block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle theta=37^(@) , with horizontal as shown in fig. find the acceleration of the block at the given instant.

A block of mass M is pulled on a smooth horizontal table by a string making an angle theta with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.

A rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30^(@) with the horizontal plane , what is the force of friction on the block ? (Take g = 10 m//s^(2) )

A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.

A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle  with the horizontal. If  is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -

A block of mass 20 kg is acted upon by a force F=30N at an angle 53^@ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2 . The friction force acting on the block by the ground is (g=10(m)/(s^2) )

A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m//s^(2)) .

A block of mass 8 kg is sliding on a surface inclined at an angle of 45^(@) with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m//s^(2) )

A block of mass 5 kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F = 20 N, making an angle of 30^(@) with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is mu=0.2 . The difference between the accelerations of the block, in case (B) and case (A) will be: (g=10ms^(-2))