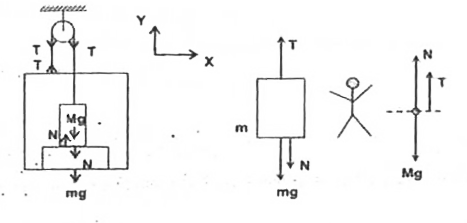
The fixed pulley is taken as frame of reference. The forces on man and box with plank are shown in figure.
The forces are as follows:
i. Weight of the man = Mg
ii. The tension in the string = T.
iii. The normal contact force between the man and the plank = N.
iv. The weight of the plank and box = mg
Referring to figure. The equation of motion of the man is given as
`T+N-Mg=Ma`
since `M gt m` and the box remains at rest, the man will have to be at rest
`T+N-Mg=0 " " ...(1)`
Similarly referring to figure,
`T-N-mg=ma=0" " ...(2)`
Solving (1) and (2) we obtain,
`T=((M+m)g)/(2) and N=((M-m)g)/(2)`