`Y+2x+Z=l " " ...(i)`
`Y+X+l_(2)+X+l_(2)+Z-l_(1)=l" "...(ii)`
Subtracting eq. `1^(st)` from eq. `2^(nd)`, we get `2l_(2)=l_(1)`
Differentiating twice this equation w.r.t time we get `therefore a_(1)=2a_(2)`
i.e. acceleration of block `m_(1)` is twice the acceleration of block `m_(2)`
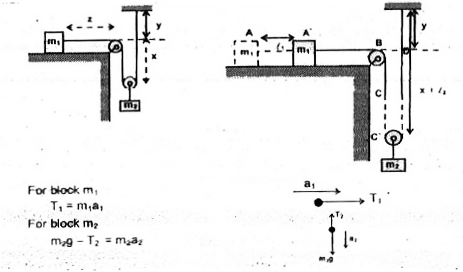
For block `m_(1)`
`T_(1)=m_(1)a_(1)`
For block `m_(2)`
`m_(2)g-T_(2)=m_(2)a_(2)`
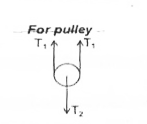
`T_(1)=T_(2) " "[because "Pulley is massless"]`
Let `a_(2)=a " " therefore t=2m_(1)a`
`therefore a_(1)=2a, " "m_(2)-2T=m_(2)a`
`T_(1)=T" Solving " a_(2)=(m_(2)g)/(m_(2)+4m_(1))`
`therefore T_(2)=2T" " therefore a_(1)=2a_(2)=(2m_(2)g)/(m_(2)+4m_(1))`