Let `x_(1) to ` distance of the pulley (wedge) from the wall.
`x_(2)to` distance of the bar from the pulley.
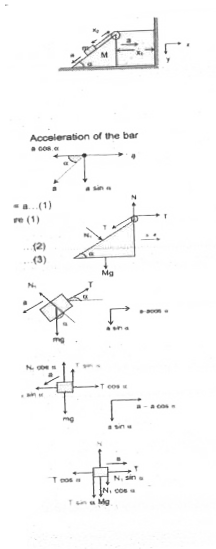
Therefore `x_(1)+x_(2)=l`
`(d^(2)x_(1))/(dt^(2)) to ` acceleration of wedge
`(d^(2)x_(1))/(dt^(2))= -(d^(2)x_(2))/(dt^(2))`
`(d^(2)x_(2))/(dt^(2)) to ` acceleration of the bar, w.r.t. wedge
`|(d^(2)x_(1))/(dt^(2))|=|(d^(2)x_(2))/(dt^(2))|=` a (say).
Net acceleration of wedge along the horizontal surface = a.... (1)
Net acceleration of bar along the horizontal surface figure (1)
`=a -` comp. of acceleration of bar w.r.t. wedge
`=a-a cos alpha " " `...(2)
Vertically downward `=a sin alpha " " `...(3)
Forces on wedge and bar are shown separately in figure(2) and fig. (3) respectively (4) and (5).
From the F.B.D. of the wedge Along the chosen X-direction `T+N_(1) sin alpha-Tcos alpha=Ma " " `...(4)
along Y-direction
For bar
`N_(1)cos alpha+T sin alpha+Mg-N=0 " " `...(5)
From the F.B.D. of the bar along X-direction
`cos alpha-N_(1) sin alpha=m.(a-acos alpha) " "`...(6)
For Wedge: along y-direction
`mg-N_(1)cos alpha-T sin alpha=m a sin alpha " " `...(7)
From equations (4), (5), (6) and (7) eliminating other quantities we can fing a. The problem can be solved by choosing X-Y axis for the system along and normal to the surface of wedge. Just do by yourself.
Hence answer is `(mg sin alpha)/(M+2m(1-cos alpha))`