Home
Class 12
PHYSICS
Two masses m(1) and m(2) are connected b...

Two masses `m_(1) and m_(2)` are connected by means of a light string, that passes over a light pulley as shown in the figure. If `m_(1)=2kg and m_(2)=5kg` and a vertical force F is applied on the pulley, then find the acceleration of the masses and that of the pulley when
(a) f = 35N, (b) F = 70N, (c) F = 140N.

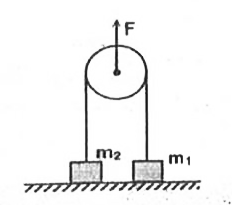
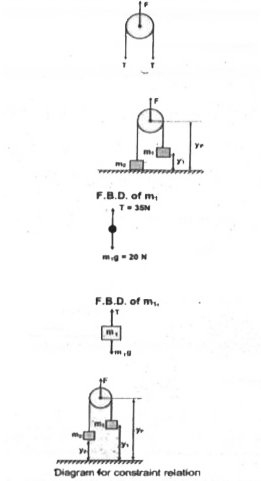
Text Solution

Verified by Experts

Since string is massless and friction is absent, hence tension in the string is same every where.
(a) Let acceleration of the pulley be `a_(p)`. For `a_(p)` to be non-zero, F.B.D. of the pulley
`T gt m_(1)g " "...(1)`
`rArr T gt 2g " " ...(2)`
From (1) and (2), we get
`F gt 2 xx (2g) rArr F gt 40N`
Therefore, when `F=35N`
`a_(p)=0` and hence `a_(1)=a_(2)=0`
As mass of the pulley is negligible
`F-2T=0`
`rArr T=F//2 rArr T=35N`
To lift `m_(2)`,
`T ge m_(2)g rArr T ge 50N`
Therefore, block `m_(2)` will not move
`rArr T-m_(1)g=m_(1)a_(1) rArr 15=2a_(1)`
`rArr a_(1)=(15)/(2)m//s^(2)`
Constraint equation
`y_(p)+y_(p)-y_(1)=` constant
`rArr 2y_(p)-y_(1)=c rArr 2(d^(2)y_(p))/(dt^(2))-(d^(2)y_(1))/(dt^(2))=0`
`rArr a_(p)=(a_(1))/(2)=(15)/(4) m//s^(2)`
(c) When F = 140N
T = 70N
`rArr T-m_(1)g=m_(1)a_(1)" " ...(1)`
`rArr 70N-20N=2xxa_(1) rArr a_(1)=25m//s^(2)`
`T-m_(2)g=m_(2)a_(2)" " ...(2)`
`rArr 70N-50N=5a_(2) rArr a_(2)=4m//s^(2)`
Constraint equation
`y_(p)-y_(2)+y_(p)-y_(1)=c`
`rArr 2y_(p)-y_(1)-y_(2)=c`
`rArr 2(d^(2)y_(p))/(dt^(2))-(d^(2)y_(1))/(dt^(2))-(d^(2)y_(2))/(dt^(2))=0`
`rArr a_(p)=(a_(1)+a_(2))/(2)=(29)/(2)m//s^(2)`
Promotional Banner

Topper's Solved these Questions

  • LAWS OF MOTION

    FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE)|17 Videos

  • LAWS OF MOTION

    FIITJEE|Exercise COMPREHENSION - I|6 Videos

  • LAWS OF MOTION

    FIITJEE|Exercise COMPREHENSION-III|2 Videos

  • KINEMATICS

    FIITJEE|Exercise NUMERICAL BASED QUESTIONS DECIMAL TYPE|5 Videos

  • MAGNETIC

    FIITJEE|Exercise Numerical Based Type|2 Videos

Similar Questions

Explore conceptually related problems

[" Two masses "m_(1)" and "m_(2)" are "],[" connected by means of a "],[" light string,that passes over "],[" a light pulley as shown in the "],[" figure.If "m_(1)=2kg" and "m_(2)=],[5kg" and a vertical force "F" is "],[" applied on the pulley then "],[" find the accelerations of the "],[" masses and that of the "],[" pulley when the force is "],[F=70N]

Two masses m_(1) and m_(2) are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m_(1) gtm_(2) acceleration of the system is:

Two unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F = 20N is applied on 1kg block find the acceleration of either block (g = 10m//s^(2)) .

Two masses m_(1) and m_(2) are attached to a string which passes over a frictionless smooth pulley. When m_(1)=10kg,m_(2)=6kg , the acceleration of masses is

Two masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of

Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :

Two masses m_(1) and m_(2) are connected by light inextensible string passing over a smooth pulley P . If the pulley moves vertically upwards with an acceleration equal to g then .

Two masses m and 2m are connected by a massless string, which passes over a pulley as shown in figure. The masses are held initially with equal lengths of the strings on either side of the pulley. Find the velocity of masses at the instant the lighter mass moves up a distance of 15m. ( g = 10 m//s^(2) )