Text Solution
Verified by Experts
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
FIITJEE|Exercise Solved Problems (Objective)|16 VideosSIMPLE HARMONIC MOTION
FIITJEE|Exercise COMPREHENSION|17 VideosSIMPLE HARMONIC MOTION
FIITJEE|Exercise Assignment Problems (Objective) (Level-II)|20 VideosSEMICONDUCTOR AND DEVICE
FIITJEE|Exercise SOLVED PROBLEMS Objective: Level-I|20 VideosTEST PAPERS
FIITJEE|Exercise PHYSICS|747 Videos
FIITJEE-SIMPLE HARMONIC MOTION-Solved Problems (Subjective)
- In the shown figure, mass m rests on smooth horizontal surface, connec...
Text Solution
|
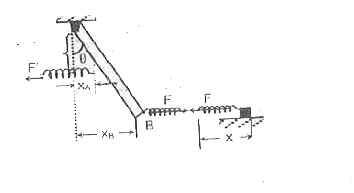
- In the string mass system shown in the figure, the string is compresse...
Text Solution
|
- A thin rod of length L and area of cross section S is pivoted at its l...
Text Solution
|
- A uniform plank of length l and mass m is balanced on a fixed semi-cir...
Text Solution
|
- A very light rod of length l pivoted at O is connected with two spring...
Text Solution
|
- A ring of mass m and radius a is connected to an inextensible string w...
Text Solution
|
- Find the frequency of small oscillations of thin uniform vertical rod ...
Text Solution
|
- Two identical balls A and B each of mass 0.1 kg are attached to two id...
Text Solution
|
- Two identical balls A and B each of mass 0.1 kg are attached to two id...
Text Solution
|
- Two identical balls A and B each of mass 0.1 kg are attached to two id...
Text Solution
|
- Consider the situation shown in the figure. A mass is hanging from a i...
Text Solution
|
- Two SHM's are represented by y(1) = A sin (omega t+ phi), y(2) = (A)/(...
Text Solution
|
- A system consisting of a smooth movable wedge of angle alpha and a blo...
Text Solution
|
_S01_031_Q01.png)