Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-MAGNETIC-Solved Problems (Subjective)
- A circular loop of radius R is bent along a diameter and given a shap...
Text Solution
|
- In a certain region surrounding the origin of the coordinate, vec(B) =...
Text Solution
|
- A particle with charge q is projected successively along the x and y a...
Text Solution
|
- Two circular loops of radii R and r (R > > r) have same cenre and carr...
Text Solution
|
- Three very long straight current carrying conductors are placed parall...
Text Solution
|
- A long thin walled hollow cylinder of radius r is carrying a current I...
Text Solution
|
- Find the current in the conductor PQ so that it remains in equilibrium...
Text Solution
|
- A long straight conductor carrying current I1 is placed in the plane o...
Text Solution
|
- In the adjoining diagram a current carrying loop pqrs is placed with i...
Text Solution
|
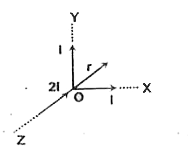
- Three semi-infinite mutually perpendicular conductors are joined at th...
Text Solution
|