लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
भौतिक विज्ञान 2012
BIHAR BOARD- PREVIOUS YEAR PAPER|Exercise खंड-II (गैर-वस्तुनिष्ठ)|19 Videosभौतिक विज्ञान -2009
BIHAR BOARD- PREVIOUS YEAR PAPER|Exercise खण्ड-II (गैर-वस्तुनिष्ट प्रश्न )(दीर्घ उत्तरीय प्रश्न)|8 Videosभौतिक विज्ञान-2011
BIHAR BOARD- PREVIOUS YEAR PAPER|Exercise खण्ड-II (गैर वास्तुनिष्ठ प्रश्न)|18 Videos
BIHAR BOARD- PREVIOUS YEAR PAPER-भौतिक विज्ञान 2012-खंड-II (गैर-वस्तुनिष्ठ)
- क्रांतिक कोण को परिभाषित करें तथा इसकी शर्तो को लिखे।
Text Solution
|
- बिंदु A तथा B के बीच समतुल्य धारिता ज्ञात करें।
Text Solution
|
- विद्युत चुंबक तथा स्थायी चुंबक के बीच दो अंतर लिखे।
Text Solution
|
- डोपिंग क्या है ?
Text Solution
|
- रेडियम की अर्द्ध-आयु 1622 वर्ष है। कितने समय बाद रेडियम के भाग का क्ष...
Text Solution
|
- ट्रांसफॉर्मर का क्रोड परतदार क्यों होता है ?
Text Solution
|
- पोलेराइड क्या है? इसके उपयोग को लिखे।
Text Solution
|
- दिये गये परिपथ में i का मान ज्ञात करें।
Text Solution
|
- विद्युत आवेश के दो मौलिक गुणों को लिखे।
Text Solution
|
- टी० वी० संकेत के प्रेषण सीमा को बढ़ाने के लिए किन्ही दो बिन्दुओ को व्यक...
Text Solution
|
- AND गेट का संकेत तथा टूथ टेबुल लिखे
Text Solution
|
- विद्युत फॉक्स का परिभाषित करें गोम के प्रमय को लिखे तथा उसे प्रमाणित क...
Text Solution
|
- धातु का 9 समी त्रिज्या वाल गात पर आवेश दिया गया। आवेशित चालक की ऊंचा...
Text Solution
|
- (1)/(f) = (mu-1) (1)/(r(1)) - (1)/(r(2)) सूत्र का स्थापित करें।
Text Solution
|
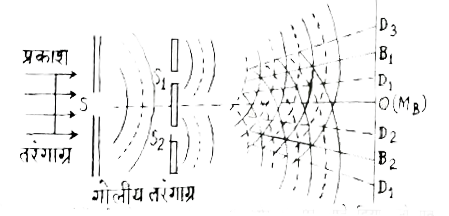
- व्यतिकरण का परिभाषित करें। यंग के द्विक छिद्र प्रयोग में फ्रिंज की चौ...
Text Solution
|
- साइक्लोट्रोन की बनावट सिद्धांत तथा कार्यविधि का संचित्र वर्णन करें।
Text Solution
|
- वायोट सावटे का नियम की व्याख्या करें । धारावाही वृत्ताकार कुंडली के के...
Text Solution
|
- रेडियो सक्रियता का परिभाषित करें। alpha,beta तथा gamma किरणों की प्रक...
Text Solution
|
- जेनर डायोड क्या है ? वोल्टता नियंत्रक के रूप में इसके उपयोग की व्याख्य...
Text Solution
|