In Young's experiment the upper slit is covered by a thin glass plate of refractive index `1.4` while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index `1.7` interference pattern is observed using light of wavelength `5400 Å`
It is found that point P on the screen where the central maximum `(n = 0)` fell before the glass plates were inserted now has `3//4` the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
.

Explanation

KEY IDEA
In Young.s double-slit experiment, slits `S_(1)` and `S_(2)` are equidistant from the source S and the slits have equal widths. Hence, light emerging from `S_(1)` and `S_(2)` has the same intensity, say `I_(0)`. Before the plates are introduced, the path difference (and hence the phase difference `phi`) at the central point P between the interfering waves is zero.
Calculation: The intensity at point P is
`I=I_(0)+I_(0)+2sqrt(I_(0)I_(0))cos 0^(@)=4I_(0)`.

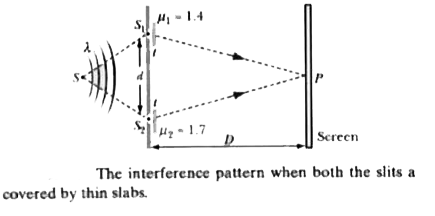
When the two plates are introduced, the path difference at the central point p between the interfering waves becomes
`Delta=(mu_(2)-1)t-(mu_(1)-1)t=(mu_(2)-mu_(1))t`.
Therefore, the phase difference is given by
`phi=(2 pi Delta)/(lambda)=(2pi)/(lambda)(mu_(2)-mu_(1))t`.
Hence, the intensity at point P becomes
`I.=I_(0)+I_(0)+2sqrt(I_(0)I_(0))cos phi=2I_(0)+2I_(0)cos phi`
It is given that
`I.=(3I)/(4)=(3)/(4) xx 4I_(0)=3I_(0)`.
Thus
`3I_(0)=2I_(0)+2I_(0)cos phi`.
Now
`cos phi=(1)/(2)`
`phi=(pi)/(3), (5pi)/(3), (7pi)/(3), (11pi)/(3), (13pi)/(3),......`
`phi=(pi)/(3)(6m +- 1)`, m= 0, 1, 2, 3,.... (35-40)
where the negative value `phi= -pi // 3` corresponding to m = 0 is not admissible since `phi` is positive as `mu_(2) gt mu_(1)`. The upward shift of the interference pattern due to the upper plate is
`(Delta y)_(1)=(mu_(1)-1)(tD)/(d)`.
The downward shift due to the lower plate is
`(Delta y)_(2)=(mu_(2)-1)(tD)/(d)`.
Therefore, the new downward shift is
`Delta y=(Delta y)_(2)-(Delta y)_(1)=(mu_(2)-mu_(1))(tD)/(d)`
`=(1.7-1.4)(tD)/(d)=(0.3 tD)/(d)`
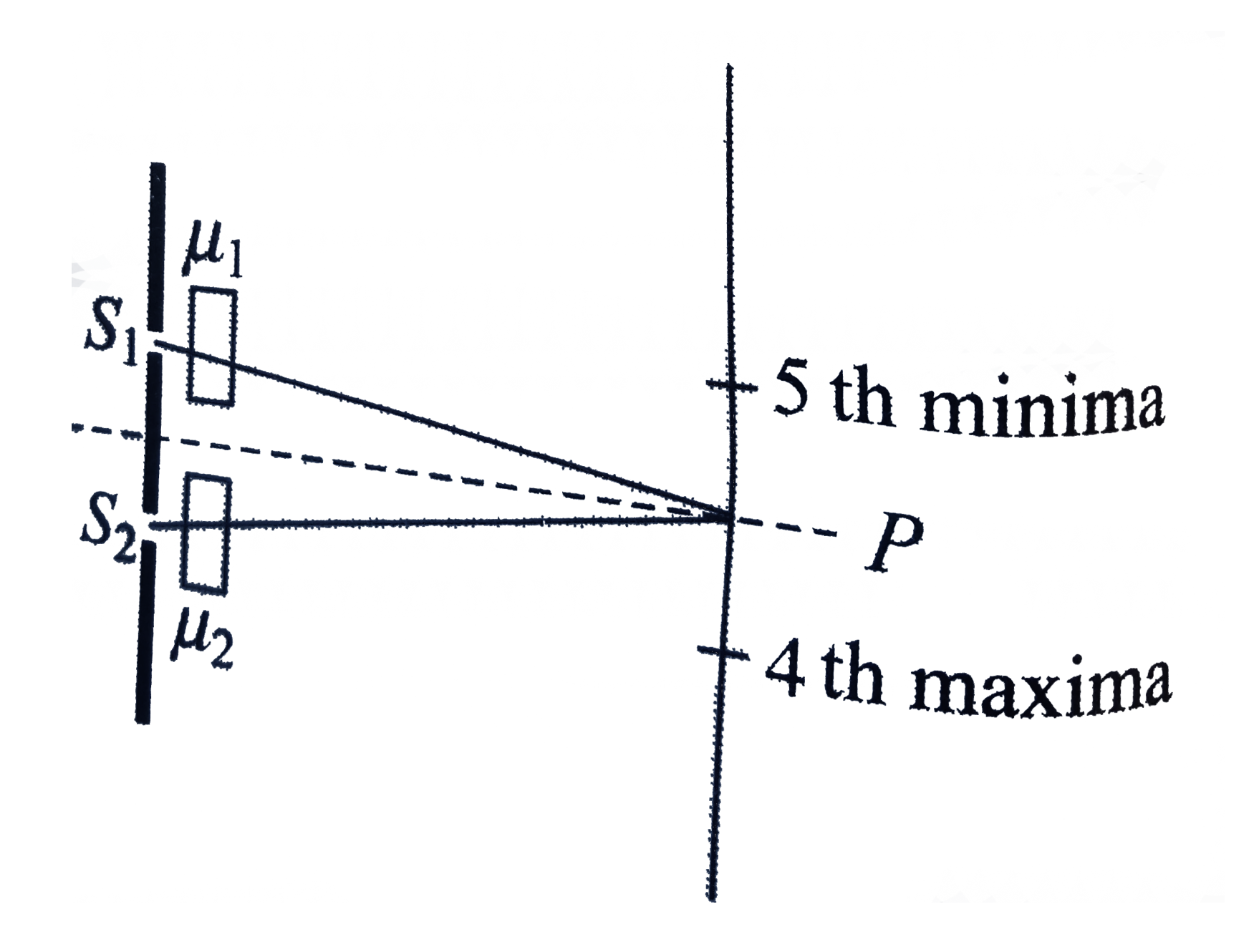
Now, the distance of the fifth maximum from P is `5 lambda D // d`, and the distance of sixth minimum from P is `[6 - (1 // 2)]lambda D // d=5.5 lambda D // d`. It is given that the net shift lies between `5 lambda D // d` and `5.5 lambda D // d`, that is
`(5lambda D)/(d) lt (0.3 tD)/(d) lt (5.5 lambda D)/(d)`
`(5lambda)/(0.3) lt t lt (5.5 lambda)/(0.3)`
`(5 xx 5.4 xx 10^(-7))/(0.3) m lt t lt (5.5 xx 5.4 xx 10^(-7))/(0.3) m`
`9.0 xx 10^(-6) m lt t lt 9.9 xx 10^(-6)m." "(35-41)`
We have seen that the phase difference,
`phi=(2pi)/(lambda)(mu_(2)-mu_(1))t`
`=(2pi)/(lambda)(1.7-1.4)t`
`=(2pi)/(lambda)(0.3)t" "(35-42)`
Using Eqs. 35-41 and 35-42, we have
`(pi)/(3)(6m +- 1)=(2pi)/(lambda)(0.3t)`
`6m +- 1=(6)/(lambda)(0.3)t=(1.8t)/(5.4 xx 10^(-7))`
`t=3(6m +- 1) xx 10^(-7) m." "(35-43)`
It is clear that Eq. 35-43 will yield a value of t which satis- fies the requirement (Eq. 35-41) if m= 5. Hence,
`t=3(6 xx 5 +- 1) xx 10^(-7)`
`=3(30 +- 1) xx 10^(-7)`
`=9.3 xx 10^(-6)m` or `8.7 xx 10^(-6)m.`
The value of `t = 8.7 xx 10^(-6)m` does not satisfy the require- ment in Eq. 35-40. Hence, `t = 9.3 xx 10^(-6) m`.