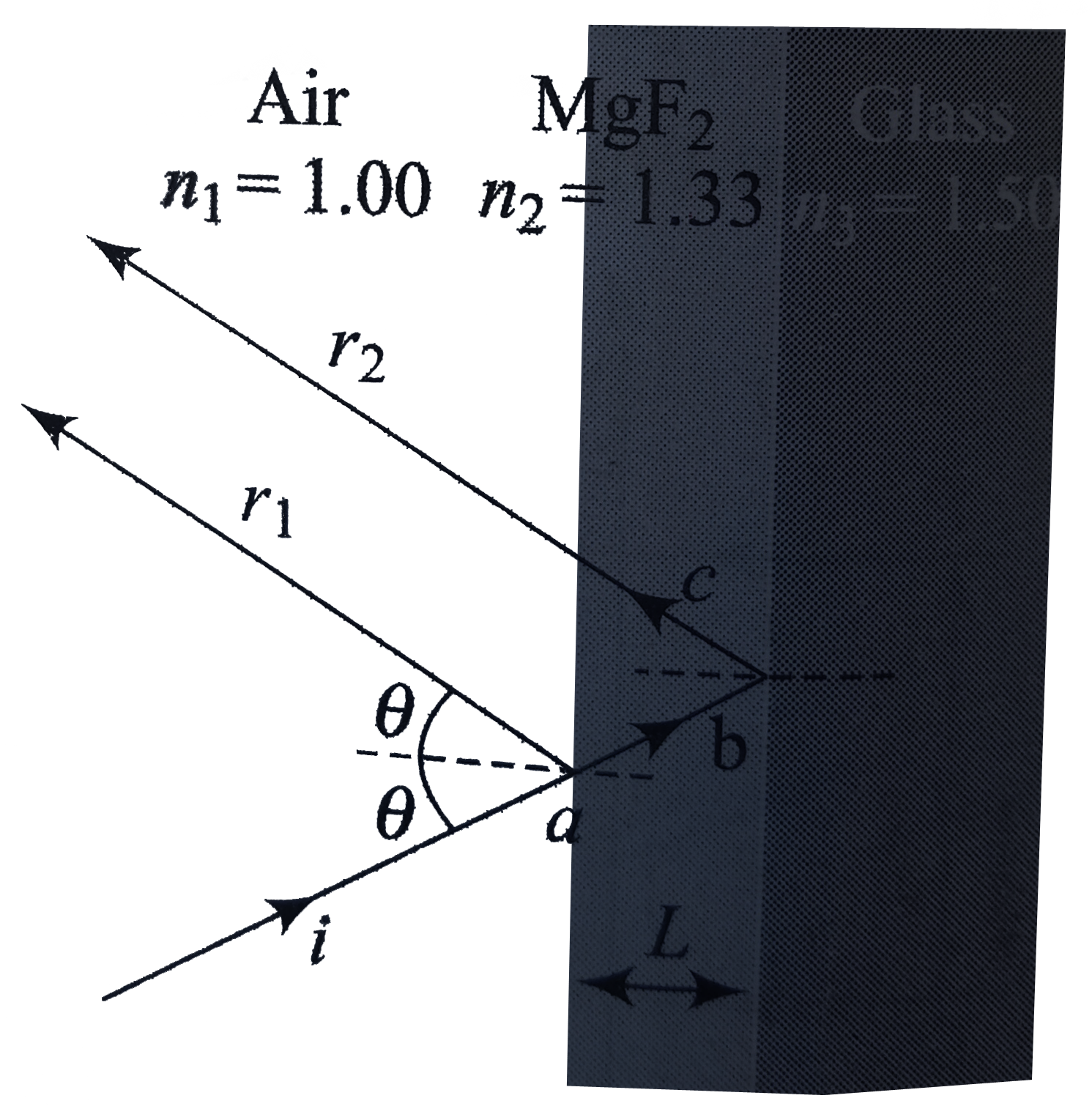Text Solution
Verified by Experts
Topper's Solved these Questions
INTERFERENCE AND DIFFRACTION
RESNICK AND HALLIDAY|Exercise CHECKPOINT|6 VideosINTERFERENCE AND DIFFRACTION
RESNICK AND HALLIDAY|Exercise PROBLEMS|61 VideosHYDROGEN ATOM
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS(Integer Type)|6 VideosMAGNETIC FIELDS DUE TO CURRENTS
RESNICK AND HALLIDAY|Exercise Practice Question (Integer Type)|4 Videos
Similar Questions
Explore conceptually related problems
RESNICK AND HALLIDAY-INTERFERENCE AND DIFFRACTION -PRACTICE QUESTIONS (Integer Type)
- A glass lens is coated on one side with a thin film of magnesium fluor...
Text Solution
|
- In the arrangement shown in the following figure, the wavelength of l...
Text Solution
|
- Light used in a Young's double-slit experiment consists of two wavele...
Text Solution
|
- In YDSE, d = 2 mm, D = 2 m, and lambda = 500 nm. If intensities of two...
Text Solution
|
- For the situation depicted in the following figure, BP - AP = lambda ...
Text Solution
|
- A thin glass plate of thickness t and refractive index mu is between s...
Text Solution
|
- In a modified Young's double-slit experiment, a monochromatic uniform ...
Text Solution
|