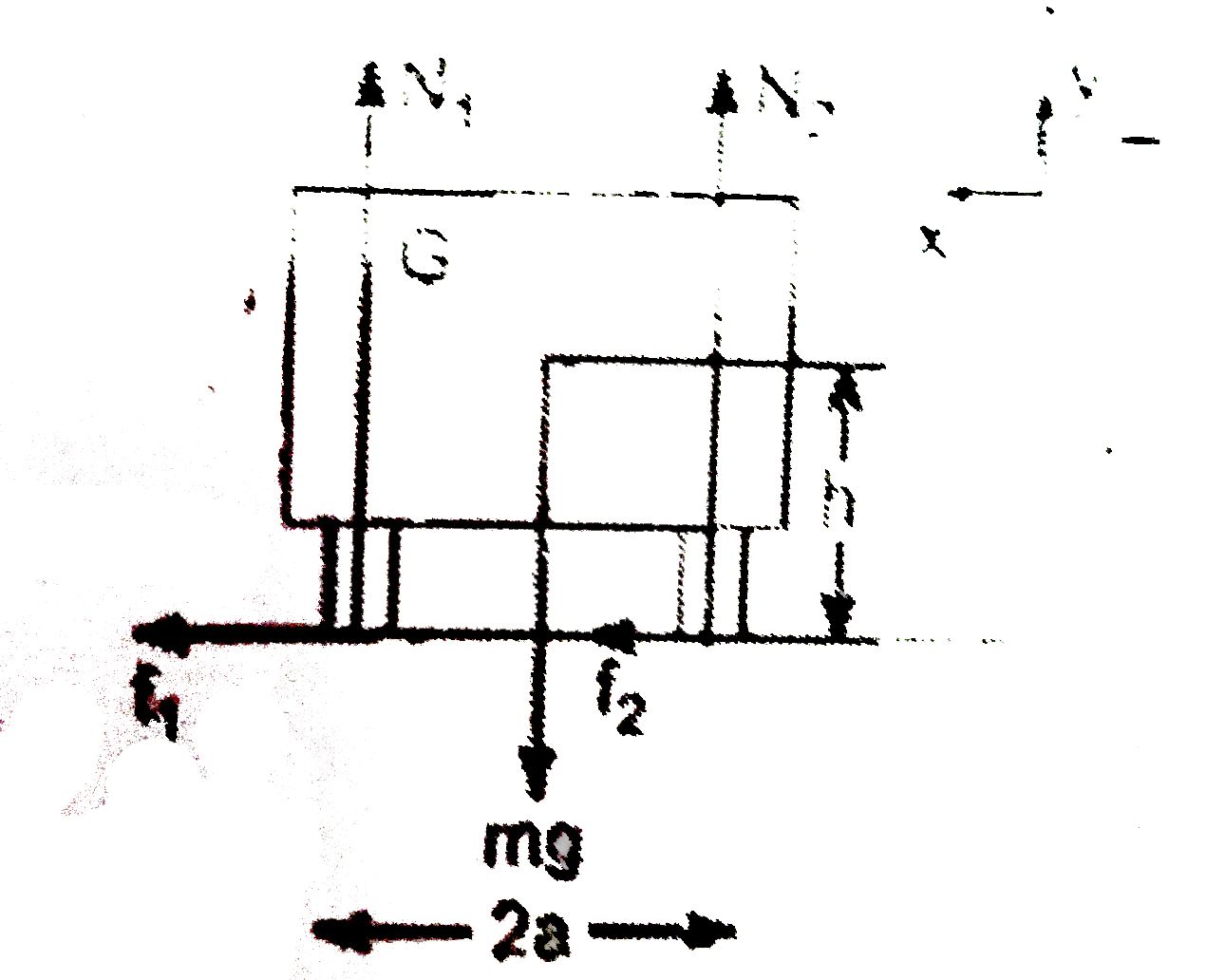Figure 11-22a shows the rear view of the car that is turn ing toward left. If you have watched any action movie where car overturns, you may know that it overturns outward of the curve when traveling at a high speed.
Frictional force on the tires provides a centripetal force while turning. When car is going at a high speed, the inner tires will lose contact with the ground. We can consider car in equilibrium in its own frame .

Calculations: As it will be a non-inertial reference frame, we need to apply pseudo centrifugal force
`sumF_(x)= F_(1)+f_(2)-(mv^(2))/(r)= 0` (11-32)
`sumF_(x)= F_(N_(1))+f_(N_(2))-mg= 0` (11-33)
From condition of rotational equilibrium, sum of moments about center of mass G must be zero:
`sumtau= (f_1+f_(2))h+ F_(N_(1))a-F_(N_(2))a=0`(11-34)
`f_(1)+ f_(2)= (F_(N_(1))-F_(N_(2)))(a)/(h)`(11-35)
On combining Eqs. 11-32 and 11-35, we can eliminate `f_(1)+ f_(2)` to obtain
`F_(N_(1))-F_(N_(2))= (mv^(2)h)/(ar)`(11-36)
Now, we can solve Eqs. 11-33 and 11-36 simultaneously to obtain
`2F_(N_(1))= mg- (mv^(2)h)/(r)` and `2F_(N_(2))= mg+ (mv^(2)h)/(r)`
The inner wheels will leave the ground when `N_(1)` becomes zero, that is,
`mg= (mv^(2)h)/(ar)`
`v^(2)= (gra)/(h)`
Learn: As expected in Eq. 11-36, we can see that as v increases the `F_(N_(1))`, will decrease and car will overturn out wardly.
If frictional force is not sufficient to provide centripetal acceleration, sideways skidding will occur instead of overturning.
`f_(1)+ f_(2) le mu(F_(N_(1))-F_(N_(2)))`
Equality sign holds when skidding starts:
`F_(N_(1))-F_(N_(2))= mg`
and `f_(1)+f_(2)= (mv^(2))/(r)`
Therefore, the limiting speed at which skidding occurs is given by `v^(2) + mugr`. If the car is to skid rather than overturn,
`mugr lt (gra)/(h)` or `mu lt (a)/(h)`