The position vectors of the vertices A, B and C of a tetrahedron ABCD are `hat i + hat j + hat k`, `hat k `, `hat i` and `hat 3i`,respectively. The altitude from vertex D to the opposite face ABC meets the median line through Aof triangle ABC at a point E. If the length of the side AD is 4 and the volume of the tetrahedron is2/2/3, find the position vectors of the point E for all its possible positfons

Answer

`-hat(i) +3hat(j) +3hat(k) " and " 3hat(i) -hat(j) -hat(k)`

Explanation

F is mid- piont of BC i.e., `F= (hat(i) +3hat(i))/(2) = 2hat(i) " and " AE bot DE`

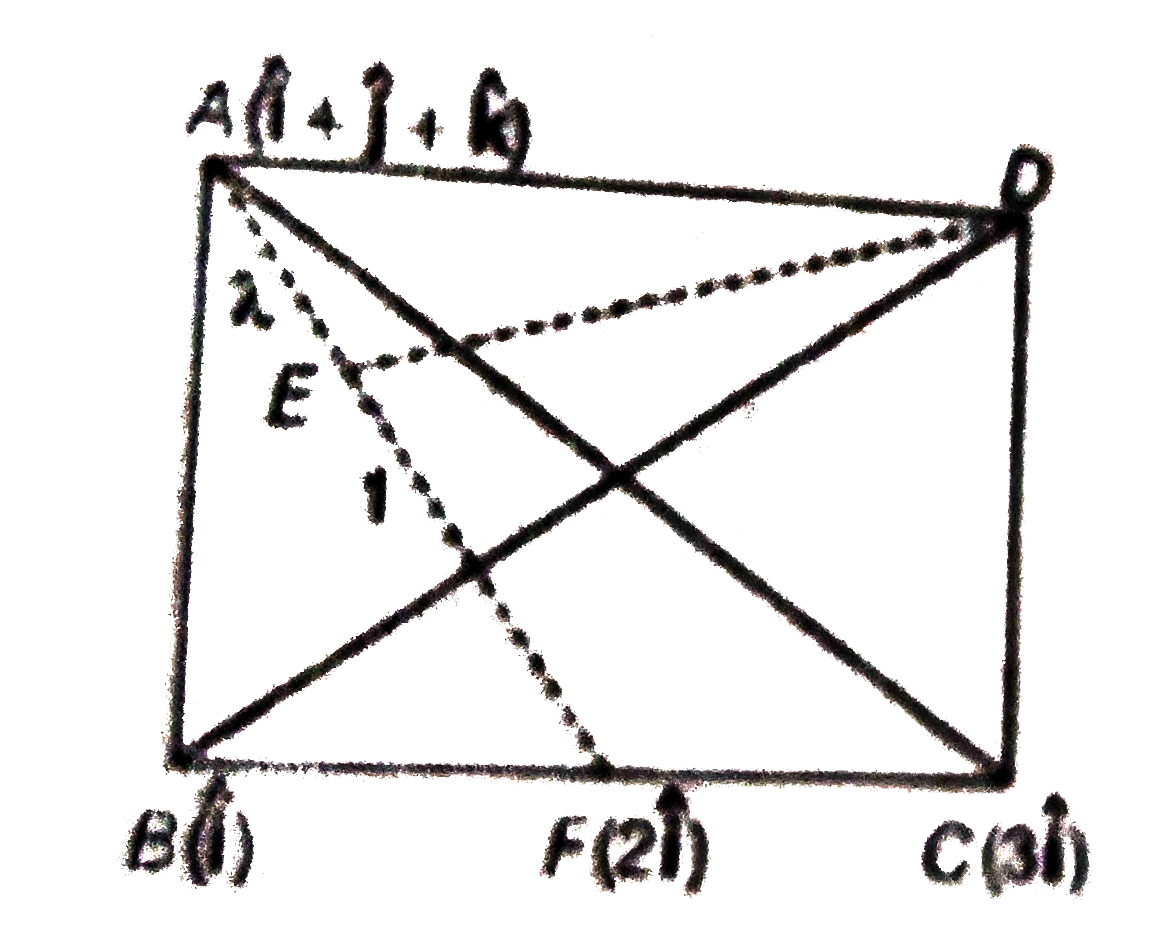
Let E divides AF in `lambda:1`. The position vectors of E is given by
`(2lambda hat(i)+ 1 (hat(i)+hat(j)+ hat(k))/(lambda +1) = ((2 lambda+1)/(lambda+1)) hat(i) + (1)/(lambda +1) hat(j) + (1)/(lambda +1) hat(k)`
Now volume of the tetrahedron
`=(1)/(3) ` (area of the bases ) (height)
`rArr (2sqrt(2))/(3)=(1)/(3) "(area of the " Delta ABC ) (DE)`
But area of the `Delta ABC =(1)/(2) |vec(BC) xx vec(BA)|`
`=(1)/(2)|2hat(i) xx (hat(j) +hat(k))|=|hat(i) xx hat(j) + hat(i) xx hat(k)| = |hat(k) - hat(j)|=sqrt(2)`
`:. (2sqrt(2))/(3)= (1)/(3) (sqrt(2)) (DE) rArr DE=2`
Since `Delta ADE` is a right angle triangle then
`rArr AD^(2) =AE^(2) +DE^(2)`
But `vec(AE) = (2lambda+1)/(lambda+1) hat(i) + (1)/(lambda+1) hat(j) + (1)/(lambda+1) hat(k) -(hat(i) +hat(j) + hat(k))`
`=(lambda)/(lambda+1) hat(i) -(lambda)/(lambda+1) hat(j) - (lambda)/(lambda+1) hat(k)`
`rArr |vec(AE)|^(2) =(1)/((lambda+1)^(2)) [lambda^(2) + lambda^(2)+lambda^(2)]= (3lambda^(2))/((lambda+1)^(2))`
Theerefore `12 =(3lambda^(2))/((lambda+1)^(2))`
`rArr 4(lambda +1)^(2) =lambda^(2) rArr 4lambda^(2) +4 + delta lambda =lambda^(2)`
`rArr 3lambda^(2) +delta lambda + 4=0 rArr 3 lambda^(2) + 6lambda +2lambda +4=0`
`rArr 3lambda(lambda+2) + 2 (lambda +2)=0`
`rArr (3lambda +2) (lambda +2) =0 rArr lambda -2 //3 . lambda =-2`
when `lambda=-2//3` position vectors of E is given by
`((2lambda +1)/(lambda+1)) hat(i) + (1)/(lambda+1) hat(j) + (1)/(lambda+1) hat(k)`
`=(2.(-2//3)+1)/(-2//3+1) hat(i) + (1)/(-2//3+1) hat(j) + (1)/(-2//3+1) hat(k)`
`=(-4//3+1)/((-2+3)/(3))hat(i) + (1)/((-2+3)/(3)) hat(j) + ( 1)/((-2+3)/(3))hat(k)`
`=((-4+3)/(3))/(1//3) hat(i) +(1)/(1//3)hat(j)+ (1)/(1//3) hat(k) =- hat(i) +3hat(j) +3hat(k)`
and when `lambda=-2 ,` position vector of E is given by
` (2xx (-2)+1)/(-2+1) hat(i) + (1)/( -2+1) hat(j) + (1)/(-2+1) hat(k) =(-4+1)/(-1) hat(i) -hat(j) -hat(k)`
`=3hat(i) -hat(j) -hat(k)`
Therefore `-hat(i) +3hat(j) +3hat(k) " and " +3hat(i) - hat(j) - hat(k)` are the answer.