(a) If the maximum acceleration that is tolerable for passengers in a subway train is `1.34 m//s^(2)` and subway stations are located 806 m apart, what is the maximum speed a subway tran can attain between stations ? (b) What is the travel time between stations ? (c) If a subway train stops for 20 s at each station, what is the maximum average speed of the train, from one start-up to the next ? (d) Graph x, v, and a versus t for the interval from one start-up to the next.

Explanation

KEY IDEA
We assume the train accelerates from rest ( `v_(0)=0` and `x_(0)=0`) at `a_(1)= +1.34 m//s^(2)` until the midway point and then deceleration at `a_(1)= -1.34 m//s^(2)` until it comes to a stop `(v_(2)=0)` at the next station. The velocity at the midpoiint is `v_(1)` , which occurs at `x_(1) = 806//2=403` m.
Calculations : (a) Equation 2-16 leads to
`v_(1)^(2) = v_(0)^(2) + 2a_(1)x_(1) rArr v_(1) = sqrt(2(1.34 m//s^(2))(403m))`
` = 32.9 m//s`.
(b) The time `t_(1)` for the accelerating stage is ( using Eq. 2-15)
`x_(1) = v_(0)t_(1) = 1/2 a_(1) t_(1)^(2) rArr t_(1) = sqrt((2(403m))/(1.34 m//s^(2)))=24.53s`.
Since the time interval for the decelerating stage turns out to be the same, we double this result and obtain `t=49.1`s for the travel time between stations.
(c) With a " dead time" of 20s, we have `T = t+20 = 69.1s`
for the total time between start-ups. Thus, Eq. 2-2 gives
`v_("avg") = (806 m)/(69.1 s) = 11.7 m//s`.
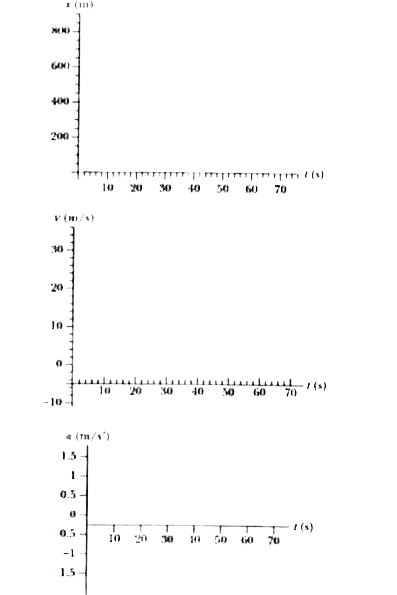
(d) The graphs for x, v and a as a function of t are shown below. The third graph , a(t), consists of three horizontal "steps" - one at `1.34 m//s^(2)` during `0 lt t lt 24.53`s, and the next at `-1.34 m//s^(2)` during `24.53 s lt t lt 49.1` s and the last at zero during the " dead time" `49.1 s lt 1 lt 69.1 s)`.