A block of mass 2.0 kg is given an initial speed along the floor towards a spring as shown. The coefficient of kinetic friction between the floor and the block is 0.4 and force constant of the spring is `5.6xx10^(3)` N/m. The block compresses the spring by 10cm before it stops for a moment. What is the initial speed (m/s) of the block?
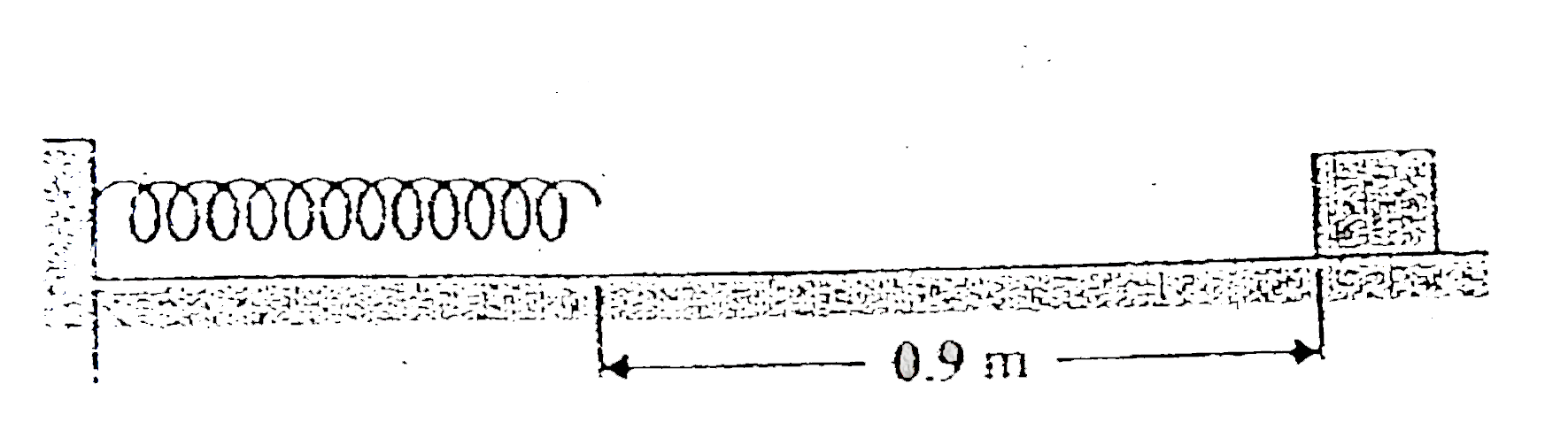
A block of mass 2.0 kg is given an initial speed along the floor towards a spring as shown. The coefficient of kinetic friction between the floor and the block is 0.4 and force constant of the spring is `5.6xx10^(3)` N/m. The block compresses the spring by 10cm before it stops for a moment. What is the initial speed (m/s) of the block?
Text Solution
Verified by Experts
Because the block is moving, a kinetic frictional force acts on it. The magnitude is given by Eq. 6-2 `(f_(k)=mu_(k)F_(N)`, where `F_(N)` is the normal force). The direction is opposite the motion (the friction opposes the sliding).
Calculating `F_(N)`: Because we need the magnitude `f_(k)` of the frictional force, we first must calculate the magnitude `F_(N)` of the normal force. Figure 6-5b is a free-body diagram showing the forces along the vertical y axis. The normal force is upward, the gravitational force with magnitude mg is downward, and (note) the vertical component `F_(y)` of the applied force is upward. That component is shown in Fig. 6-5c, where we can see that `F_(y)=Fsintheta`. We can write Newton.s second law `(F_("net"=mveca))` for those forces along the y axis as
`F_(N)+Fsintheta-mg=m(0),`

Figure 65 (a) A force is applied to a moving block. (b) The vertical forces. (c) The components of the applied force. (d) The horizontal forces and acceleration.
where we substituted zero for the acceleration along the y axis (the block does not even move along that axis). Thus,
`F_(N)=mg-Fsintheta`.
Calculating acceleration a: Figure 6-5d is a free-body diagram for motion along the x axis. The horizontal component `F_(x)` of the applied force is rightward, from Fig. 6-5c, we see that `F_(x)=Fcostheta`. The frictional force has magnitude `f_(x)(=kF_(N))` and is leftward. Writing Newton.s second law for motion along the x axis gives us
`Fcostheta-mu_(k)F_(N)=ma`
Substituting for `F_(N)` from Eq. 6-15 and solving for a lead to
`a=(F)/(m)costheta-mu_(k)(g-(F)/(m)sintheta)`
Finding a maximum: To find the value of `theta` that maximizes a, we take the derivative of a with respect to `theta` and set the result equal to zero:
`(da)/(d""theta)=-(F)/(m)sintheta+mu_(k)(F)/(m)costheta=0`.
Rearranging and using the identity `(sintheta)//(costheta)=tantheta` give us
`tantheta=mu_(k)`.
Solving for `theta` and substituting the given `mu_(k)=0.40`, we find that the acceleration will be maximum if
`theta=tan^(-1)mu_(k)`
Comment: As we increase `theta` from 0, more of the applied force `vecF` is upward, relieving the normal force. The decrease in the normal force causes a decrease in the frictional force, which opposes the block.s motion. Thus, the block.s acceleration tends to increase. However, the increase in `theta` also decreases the horizontal component of `vecF`, and so the block.s acceleration tends to decrease. These opposing tendencies produce a maximum acceleration at `theta= 22^(@)`
Calculating `F_(N)`: Because we need the magnitude `f_(k)` of the frictional force, we first must calculate the magnitude `F_(N)` of the normal force. Figure 6-5b is a free-body diagram showing the forces along the vertical y axis. The normal force is upward, the gravitational force with magnitude mg is downward, and (note) the vertical component `F_(y)` of the applied force is upward. That component is shown in Fig. 6-5c, where we can see that `F_(y)=Fsintheta`. We can write Newton.s second law `(F_("net"=mveca))` for those forces along the y axis as
`F_(N)+Fsintheta-mg=m(0),`

Figure 65 (a) A force is applied to a moving block. (b) The vertical forces. (c) The components of the applied force. (d) The horizontal forces and acceleration.
where we substituted zero for the acceleration along the y axis (the block does not even move along that axis). Thus,
`F_(N)=mg-Fsintheta`.
Calculating acceleration a: Figure 6-5d is a free-body diagram for motion along the x axis. The horizontal component `F_(x)` of the applied force is rightward, from Fig. 6-5c, we see that `F_(x)=Fcostheta`. The frictional force has magnitude `f_(x)(=kF_(N))` and is leftward. Writing Newton.s second law for motion along the x axis gives us
`Fcostheta-mu_(k)F_(N)=ma`
Substituting for `F_(N)` from Eq. 6-15 and solving for a lead to
`a=(F)/(m)costheta-mu_(k)(g-(F)/(m)sintheta)`
Finding a maximum: To find the value of `theta` that maximizes a, we take the derivative of a with respect to `theta` and set the result equal to zero:
`(da)/(d""theta)=-(F)/(m)sintheta+mu_(k)(F)/(m)costheta=0`.
Rearranging and using the identity `(sintheta)//(costheta)=tantheta` give us
`tantheta=mu_(k)`.
Solving for `theta` and substituting the given `mu_(k)=0.40`, we find that the acceleration will be maximum if
`theta=tan^(-1)mu_(k)`
Comment: As we increase `theta` from 0, more of the applied force `vecF` is upward, relieving the normal force. The decrease in the normal force causes a decrease in the frictional force, which opposes the block.s motion. Thus, the block.s acceleration tends to increase. However, the increase in `theta` also decreases the horizontal component of `vecF`, and so the block.s acceleration tends to decrease. These opposing tendencies produce a maximum acceleration at `theta= 22^(@)`
Topper's Solved these Questions
FORCE AND MOTION-II
RESNICK AND HALLIDAY|Exercise CHECKPOINTS|5 VideosFORCE AND MOTION-II
RESNICK AND HALLIDAY|Exercise PROBLEMS|33 VideosFORCE AND MOTION - I
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|3 VideosGAUSS' LAW
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (INTEGER TYPE)|3 Videos
Similar Questions
Explore conceptually related problems
A block of mass 2 kg, initially at rest on a horizontal floor, is now acted upon by a horizontal force of 10 N . The coefficient of friction between the block and the floor is 0.2. If g = 10 m//s^(2) , then :
A block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k = 100 N//m with a velocity 2 m//s , the maximum compression of the spring is
A block of mass 0.18 kg is attached to a spring of force constant 2N/m. The coefficient of friction between the block and the floor is 0.1. Initially, the block is at rest and the spring is unstretched. An impulse is given to the block. The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is v=N/10. Then, N is
A block of mass m is moving with a speed v on a horizontal rought surface and collides with a horizontal monted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is mu The maximum cobnpression of the spring is
A block of mass 1 kg moves towards a spring of force constant 10 N//m . The spring is massless and unstretched. The coeffcient of friction between block and surface is 0.30 . After compressing the spring, block does not return back : (g = 10 m//s) .
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g = 10 m//s^(2) )
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10 m s^(-2) )