Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-TRIANGLES -DO THIS
- There are some statements given below. Write whether they are true or ...
Text Solution
|
- There are some statements given below. Write whether they are true or ...
Text Solution
|
- There are some statements given below. Write whether they are true or ...
Text Solution
|
- There are some statements given below. Write whether they are true or ...
Text Solution
|
- Which minimum measurements do you require to check if the given figure...
Text Solution
|
- State whether the following triangles are congruent or not? Give reaso...
Text Solution
|
- State whether the following triangles are congruent or not? Give reaso...
Text Solution
|
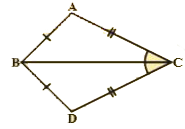
- In the adjacent figure DeltaABC and DeltaDBC are two triangles such th...
Text Solution
|
- Draw a triangle ABC and measure its sides.
Text Solution
|