Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-AREAS -EXERCISE 11.1
- In DeltaABC, angleABC = 90^@ , AD = DC, AB = 12cm and BC = 6.5 cm. Fi...
Text Solution
|
- Find the area of a quadrilateral PQRS in which angleQPS = angleSQR = 9...
Text Solution
|
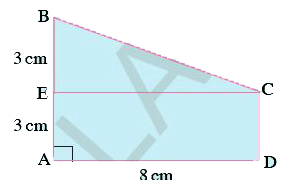
- Find the area of trapezium ABCD as given in the figure in which ADCE i...
Text Solution
|
- ABCD is a parallelogram. The diagonals AC and BD intersect each other ...
Text Solution
|