Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-SIMILAR TRIANGLES -EXERCISE - 8.4
- Prove that the sum of the squares of the sides of a rhombus is equal t...
Text Solution
|
- ABC is a right triangle right angled at B. Let D and E be any points ...
Text Solution
|
- Prove that three times the square of any side of an equilateral triang...
Text Solution
|
- PQR is a triangle right angled at P and M is a point on QR such that P...
Text Solution
|
- ABD is a triangle right angled at A and AC bot BD Show that (i) AB...
Text Solution
|
- ABC is an isosceles triangle right angled at C. Prove that AB^(2) = 2...
Text Solution
|
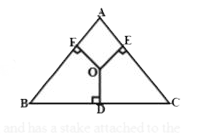
- ‘O’ is any point in the interior of a triangle ABC. If OD bot BC, OE ...
Text Solution
|
- A wire attached to a vertical pole of height 18m is 24m long and has a...
Text Solution
|
- Two poles of heights 6m and 11m stand on a plane ground. If the dista...
Text Solution
|
- In an equilateral triangle ABC, D is a point on side BC such that BD =...
Text Solution
|
- In the given figure, ABC is a triangle right angled at B. D and E are...
Text Solution
|
- ABC is an isosceles triangle right angled at B. Similar triangles ACD...
Text Solution
|
- Equilateral triangles are drawn on the three sides of a right angled t...
Text Solution
|
- Prove that the area of the equilateral triangle described on the side ...
Text Solution
|