Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-BINOMIAL THEOREM-SOLVED EXAMPLES
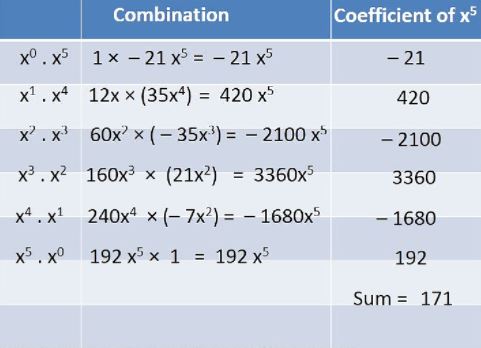
- Find the coefficient of x^5 in the expansioin of the product (1+2x)^6(...
Text Solution
|
- The coefficients of three consecutive terms in the expansion of (1+a)...
Text Solution
|
- The second, third and fourth terms in the binomial expansion (x+a)^na...
Text Solution
|
- Which is larger (1. 01)^(10000000)or 10,000?
Text Solution
|
- Compute (98)^5.
Text Solution
|
- Expand (x^2+3/x)^4,x!=0
Text Solution
|
- Find the coefficient of x^6y^3in the expansion of (x+2y)^9.
Text Solution
|
- Show that the middle term in the expansion of (1+x)^(2n) is (1. ...
Text Solution
|
- Find a if the 17^(t h)and 18^(t h)terms of the expansion (2+a)^(50)are...
Text Solution
|
- Using binomial theorem, prove that 6^n-5nalways leaves remainder 1 wh...
Text Solution
|
- Find the term independent of x in the expansion of (3/2x^2-1/(3x))^6.
Text Solution
|
- If the coefficients of a^(r-1),a^rand a^(r+1)in the expansion of (1+a...
Text Solution
|
- Show that the coefficient of the middle term in the expansion of (1+x...
Text Solution
|
- Find the coefficient of a^4in the product (1+2a)^4(2-a)^5using binomi...
Text Solution
|
- Find the r^(t h)term from the end in the expansion of (x+a)^n.
Text Solution
|
- Find the term independent of x in the expansion of (root(3)(x) + 1/(2...
Text Solution
|
- The sum of the coefficients of the first three terms in the expansion...
Text Solution
|
- If the coefficients of (r-5)^(th) and (2r-1)^(t h)terms of the expans...
Text Solution
|