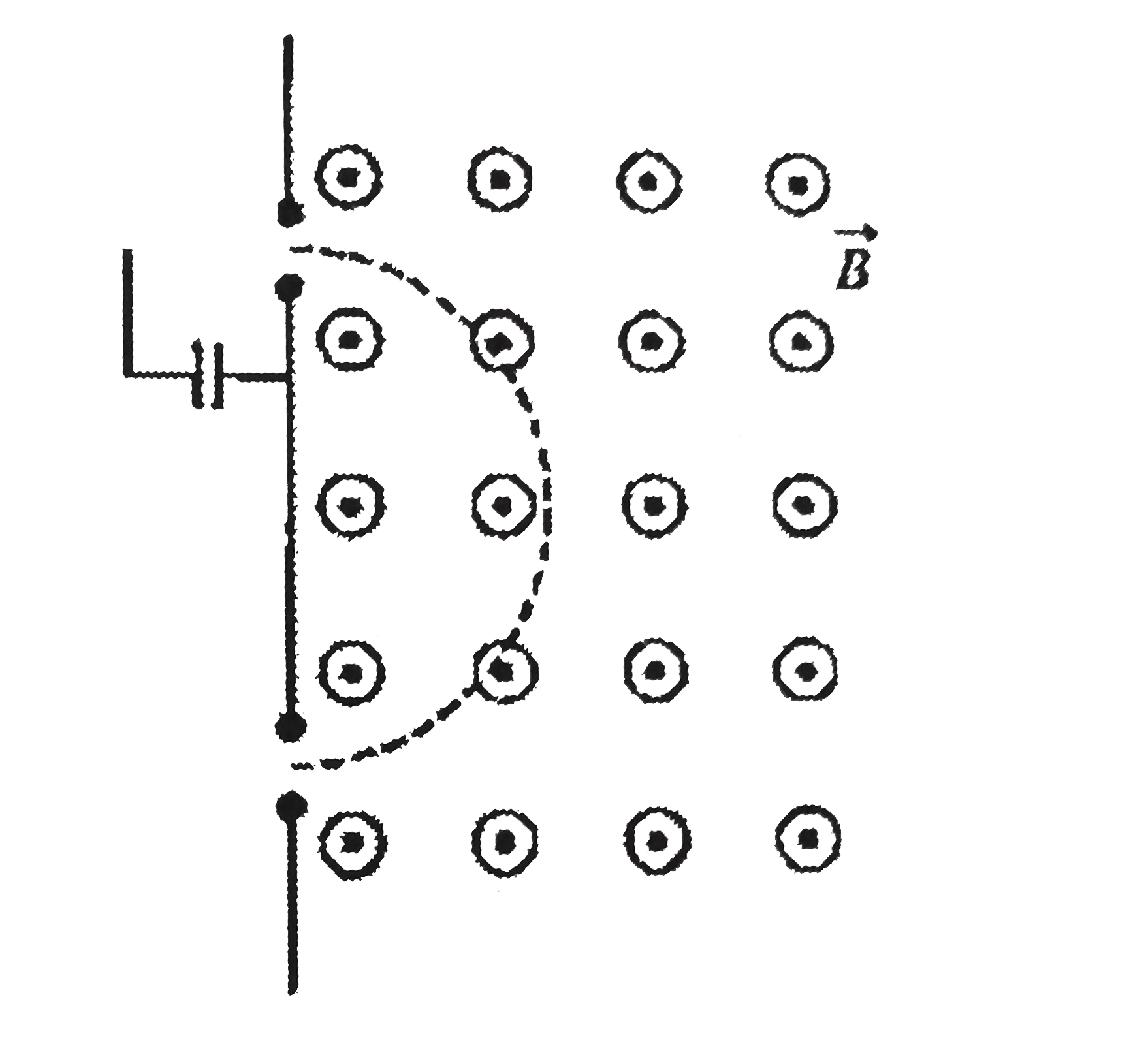
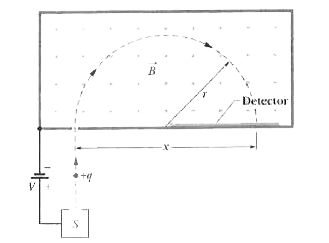
Text Solution
Verified by Experts
Topper's Solved these Questions
MAGNETIC FORCE
RESNICK AND HALLIDAY|Exercise Check point|6 VideosMAGNETIC FORCE
RESNICK AND HALLIDAY|Exercise Problems|49 VideosMAGNETIC FIELDS DUE TO CURRENTS
RESNICK AND HALLIDAY|Exercise Practice Question (Integer Type)|4 VideosMOTION ALONG A STRAIGHT LINE
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS ( Integer Type )|3 Videos
Similar Questions
Explore conceptually related problems
RESNICK AND HALLIDAY-MAGNETIC FORCE-Practice Questions (Integer type )
- A mass spectrometer is a device which selelct particle of equal mass. ...
Text Solution
|
- A steel wire of length l has a magnetic moment M. It is bent into a se...
Text Solution
|
- A bar magnet suspended freely has period of oscillation of 2s. Now, th...
Text Solution
|
- Two bar magnets of equal length and equal magnetic moment are placed a...
Text Solution
|
- Two equal magnetic poles placed 10 cm apart in air attract each other ...
Text Solution
|
- The work done in turning a magnet of magnetic moment M by an angle of ...
Text Solution
|
- At a certain place, a magnet makes 30 oscillations per minute. At anot...
Text Solution
|
- A bar magnet has a magnetic moment of 2.5 J/T and is placed in a magne...
Text Solution
|