KEY IDEA
The light beam is incident on the sphere as a parallel beam. However, since the normal at every point in not parallel to the normal at other points, the beam will not be reflected as a parallel beam.
Calculation : For the analysis, let us consider a small element of surface at angle q to horizontal direction. This element of the shape of ring subtends an angle dq at the center as shown in Fig.
The momentum of a photon is
`p=(h)/(lambda)`.
From symmetry, we can say that the impulse on the sphere in all direction perpendicular to incident beam directionis zero. The momentum of the photon in x direction changes as can be seen in Fig. Therefore,
`Deltap_(x)=(h)/(lambda)-(-(h)/(lambda)cos 2theta)`
`=(h)/(lambda)(1+cos 2 theta)=(h)/(lambda)xx2cos^(2)theta`.
The number of photons incident unit time on this element is given by
`(IdAxxlambda)/(hc)`
The number of photons incident unit time on this elemetn is given by
`(IdAxxlambda)/(hc)`
Note carefully that dA is a cross - section area of incident beam and not the element of the sphere. Area of the element is given by
`dA_(e)=Rd thetaxx2piR sin theta`
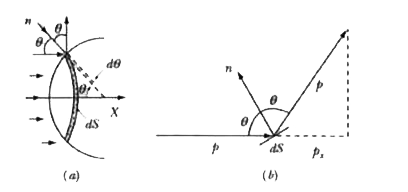
(a) A plane beam is incident on a perfectly reflecting sphere (b) Change in momentum of a photon.
Therefore, the area of cross - section of incident beam would be lesser by a factor of `cos theta`.
`dA=2piR^(2)sin theta d theta xx cos theta`
Thus,
`dF=("Number of photons incident")/("Time")xxDeltap_(x)`
`=(Ixx2piR^(2)sin theta cos theta d theta)/(hc)xxlambdaxx(h)/(lambda)xx2cos^(2)theta`
`=(4piR^(2)I)/(c)cos^(3)theta sin theta d theta`.
Also,
`F int dF`
`=(4piR^(2)I)/(c)int_(0)^(pi//2)cos^(3)theta sin theta d theta`
`=(piR^(2)I)/(c)`
Note : If the sphere were a perfect absorber, the force exerted by light beam on the sphere would be the same.
