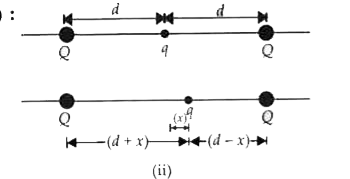
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTROSTATICS
MTG-WBJEE|Exercise (WB JEE Previous Years Questions ) CATEGORY 3 : One or More than One Opion correct Type|4 VideosELECTROSTATICS
MTG-WBJEE|Exercise (WB JEE Previous Years Questions ) CATEGORY 1 : Single Option correct Type|23 VideosELECTROMAGNETIC WAVES
MTG-WBJEE|Exercise WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)|10 VideosGRAVITATION
MTG-WBJEE|Exercise WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type|7 Videos
Similar Questions
Explore conceptually related problems
MTG-WBJEE-ELECTROSTATICS-(WB JEE Previous Years Questions ) CATEGORY 2 : Single Option correct Type
- A sphere of radius R has a volume density of charge rho=kr, were r is ...
Text Solution
|
- A particle of mass m and charge q is located midway between two fixed ...
Text Solution
|
- A charge q is placed at one corner of cube. The elctric flux through a...
Text Solution
|
- A particle with charge Q coulomb, tied at the end of an inextensible s...
Text Solution
|
- A unit negative charge with mass resides at the midpoint of the straig...
Text Solution
|
- A particle with charge e and mass m, moving along the X-axis with a un...
Text Solution
|
- The insulated plates of a charged parallel plate capacitor (with small...
Text Solution
|
- The bob of a pendulum of mass 'm' suspended by an inextensible string ...
Text Solution
|