A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 4 ROTATION OF A COMPLEX NUMBER (OBJECTIVE QUESTION II)(ONE OR MORE THAN ONE CORRECT OPTION)|2 VideosCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 4 ROTATION OF A COMPLEX NUMBER (FILL IN THE BLANKS )|3 VideosCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 ARGUMENT OF A COMPLEX NUMBER (OBJECTIVE QUESTIONS II)(ANALYTICAL & DESCRIPTIVE QUESTIONS )|1 VideosCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 5 Integer Answer type Question|1 VideosDEFINITE INTEGRATION
IIT JEE PREVIOUS YEAR|Exercise LIMITS AS THE SUM|6 Videos
IIT JEE PREVIOUS YEAR-COMPLEX NUMBERS-TOPIC 4 ROTATION OF A COMPLEX NUMBER (OBJECTIVE QUESTION I)(ONLY ONE CORRECT OPTION)
- If z=((sqrt(3))/2+i/2)^5+((sqrt(3))/2-i/2)^5 , then prove that I m(z)=...
Text Solution
|
- A particle starts from a point z0=1+i where i=sqrt(-1). lt moves horiz...
Text Solution
|
- A man walks a distance of 3 units from the origin towards north-east t...
Text Solution
|
- The shaded region ,where P=(-1 ,0)Q=(-1 + sqrt(2),sqrt(2)) R=(-1+sq...
Text Solution
|
- If 0 lt alpha lt pi/2 is a fixed andgle .If P=(cos theta sin theta) an...
Text Solution
|
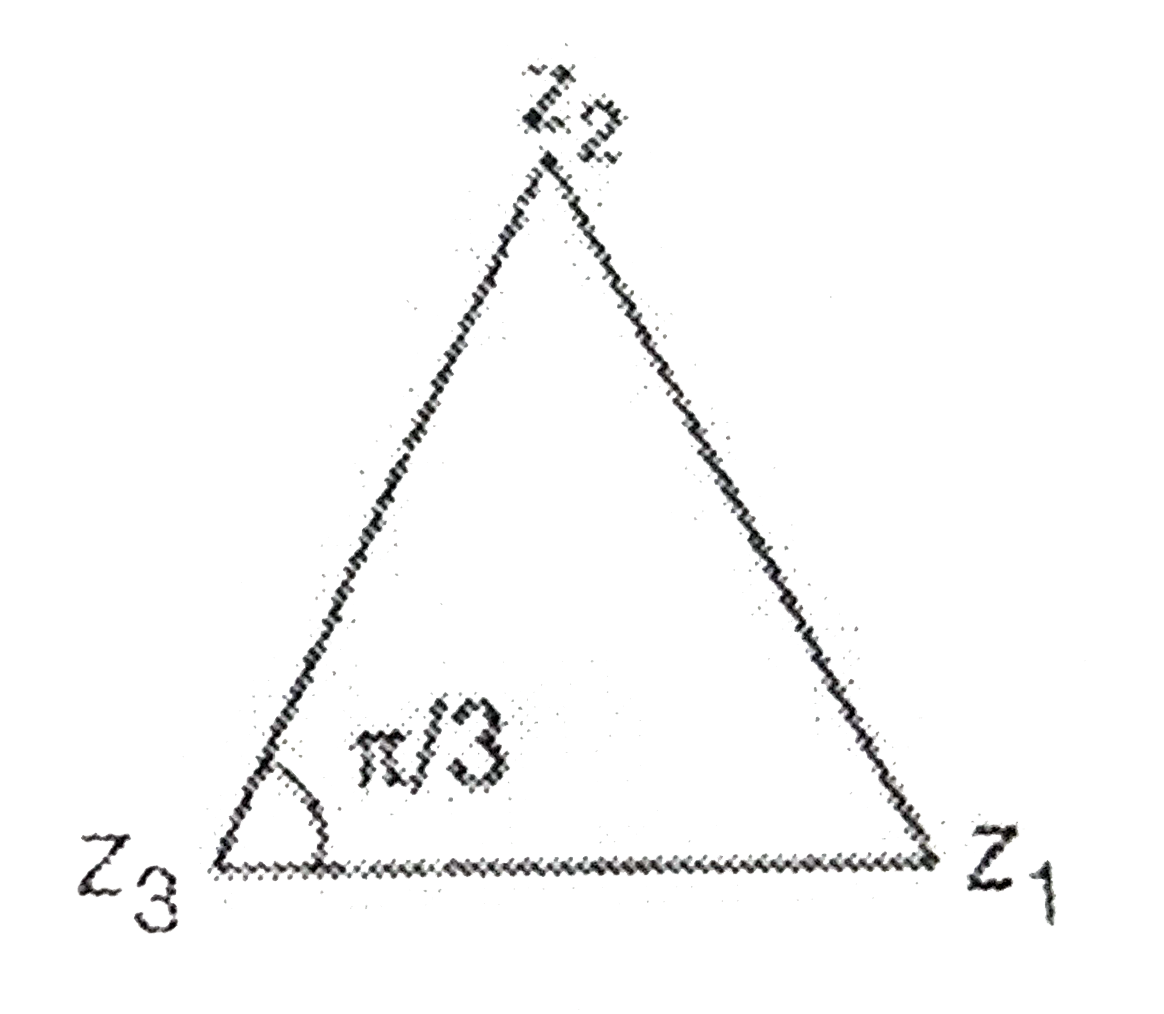
- The complex numbers z1 z2 and z3 satisfying (z1-z3)/(z2-z3) =(1- i sqr...
Text Solution
|