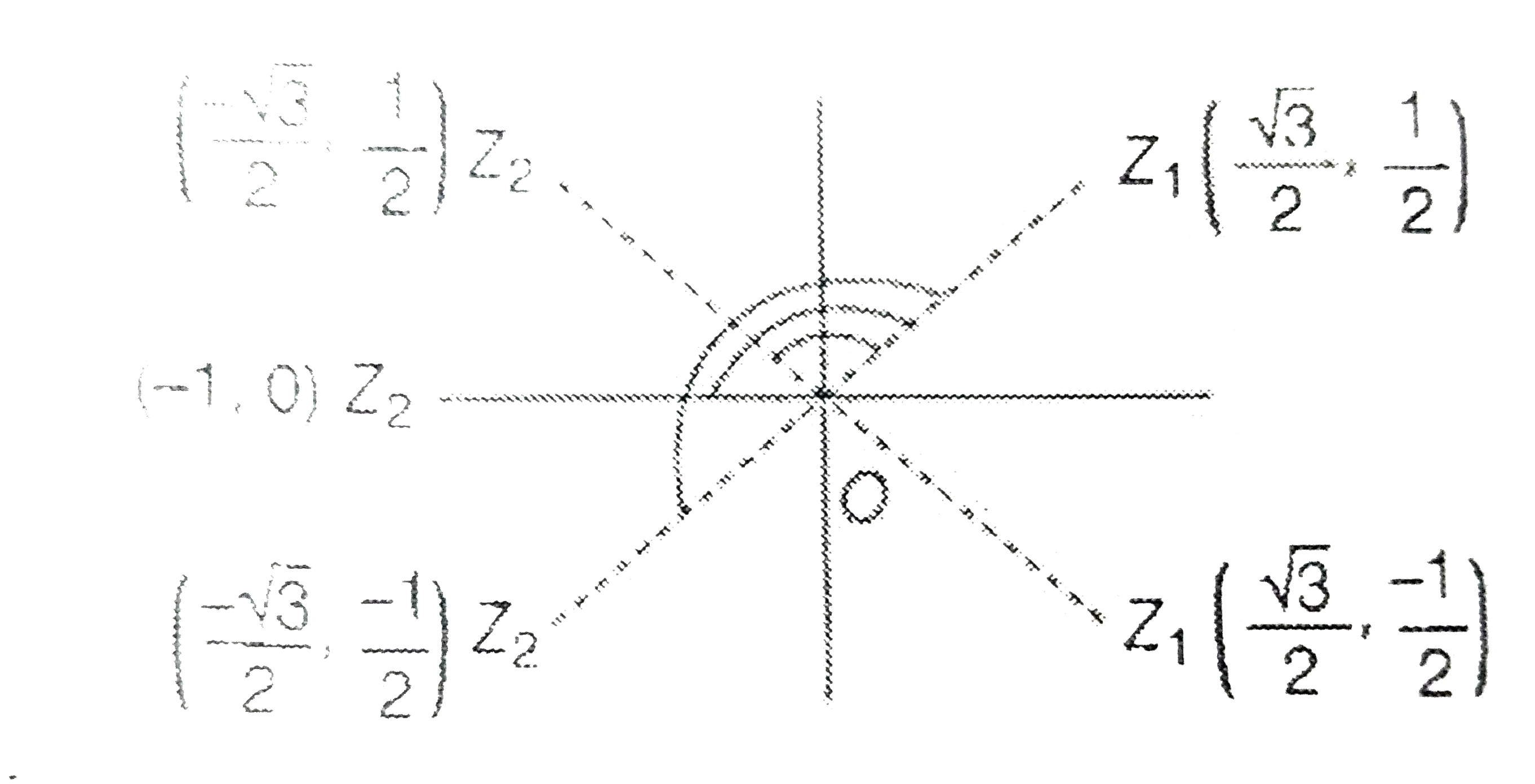A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 4 ROTATION OF A COMPLEX NUMBER (FILL IN THE BLANKS )|3 VideosCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 4 ROTATION OF A COMPLEX NUMBER (ANALYTICAL & DESCRIPTIVE QUESTIONS)|7 VideosCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 4 ROTATION OF A COMPLEX NUMBER (OBJECTIVE QUESTION I)(ONLY ONE CORRECT OPTION)|6 VideosCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 5 Integer Answer type Question|1 VideosDEFINITE INTEGRATION
IIT JEE PREVIOUS YEAR|Exercise LIMITS AS THE SUM|6 Videos
Similar Questions
Explore conceptually related problems