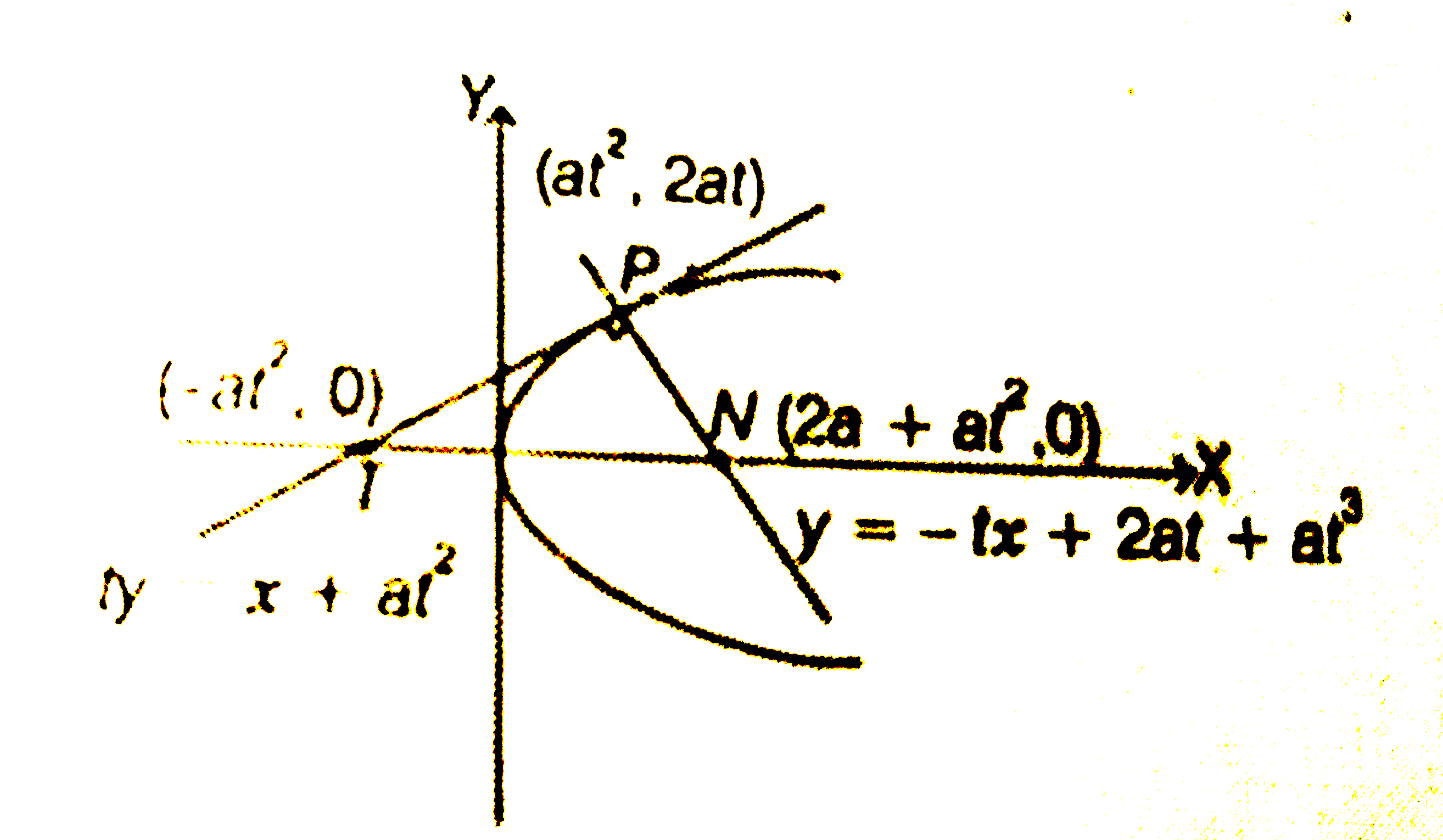Home
Class 12
MATHS
The tangent PT and the normal PN to the ...

The tangent PT and the normal PN to the parabola `y^2=4ax` at a point P on it meet its axis at points T and N, respectively. The locus of the centroid of the triangle PTN is a parabola whose:

A

vertex is `((2a)/(3),0)`

B

directrix is x = 0

C

latusrectum is `(2a)/(3)`

D

focus is (a,0)

Text Solution

Verified by Experts

The correct Answer is:
A, D
Equation of tangent and normal at point `P(at^(2), 2at)` is
`ty = x = at^(2)` and `y = - tx + 2at + at^(2)`
Let controid of `Delta PTN` is R(h,k)
`:. H = (at^(2) + (-at^(2)) + 2a + at^(2))/(3)`

and `k = (2at)/(3)`
`implies 3h = 2a + a ((3k)/(2a))^(2)`
`implies 3h = 2a + (9k^(2))/(4a)`
`implies 9k^(2) = 4a (3h - 2a)`
`:.` Locus of centroid is
`y^(2) = (4a)/(3) (x - (2a)/(3))`
`:.` vertex `((2a)/(3), 0)`, directrix
`x - (2a)/(3) = - (a)/(3)`
`implies x = (a)/(3)`
and latusrectum `= (4a)/(3)`
`:.` Focus `((a)/(3) + (2a)/(3), 0)` i.e., (a,0)
Promotional Banner

Topper's Solved these Questions

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (INTEGER )|1 Videos

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ANALYTICAL & DESCRIPTIVE )|4 Videos

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS I (MATCH THE COLUMNS )|1 Videos

  • MISCELLANEOUS

    IIT JEE PREVIOUS YEAR|Exercise MISCELLANEOUS|87 Videos

  • PERMUTATIONS AND COMBINATIONS

    IIT JEE PREVIOUS YEAR|Exercise Dearrangement and Number of Divisors (Fill in the Blank )|1 Videos

Similar Questions

Explore conceptually related problems

The tangent and normal at the point P(4,4) to the parabola, y^(2) = 4x intersect the x-axis at the points Q and R, respectively. Then the circumcentre of the DeltaPQR is

The normal to the parabola y^(2)=8ax at the point (2, 4) meets the parabola again at the point

TP and TQ are tangents to parabola y^(2)=4x and normals at P and Q intersect at a point R on the curve.The locus of the centre of the circle circumseribing Delta TPQ is a parabola whose

The tangent and normal at P(t), for all real positive t, to the parabola y^(2)=4ax meet the axis of the parabola in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle passing through the points P, Tand G is

From a variable point R on the line y = 2x + 3 tangents are drawn to the parabola y^(2)=4ax touch it at P and Q point. Find the locus of the centroid of the triangle PQR.

The normal meet the parabola y^(2)=4ax at that point where the abscissa of the point is equal to the ordinate of the point is

Tangent and normal at any point P of the parabola y^(2)=4ax(a gt 0) meet the x-axis at T and N respectively. If the lengths of sub-tangent and sub-normal at this point are equal, then the area of DeltaPTN is given by