Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
RESNICK AND HALLIDAY|Exercise Check points|9 VideosELECTRIC CHARGES AND FIELDS
RESNICK AND HALLIDAY|Exercise Problems|63 VideosELASTICITY
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|3 VideosELECTRIC POTENTIAL
RESNICK AND HALLIDAY|Exercise (PRACTICE QUESTIONS) Integer Type|1 Videos
Similar Questions
Explore conceptually related problems
RESNICK AND HALLIDAY-ELECTRIC CHARGES AND FIELDS-Practice Questions (Integer Type )
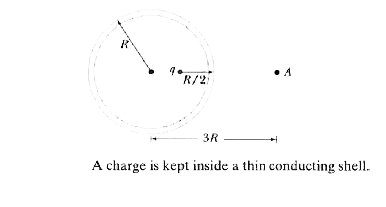
- Find the electric field at (A) (a) due to q, (b) due to charges induce...
Text Solution
|
- A point charge q = 1 C and mass 1 kg is projected with speed 10 m//...
Text Solution
|
- Two spherical objects are separated by a distance of 1.80 xx 10^(-3) m...
Text Solution
|
- An electric dipole, made up of a positive and negative charge, each of...
Text Solution
|