Home
Class 10
MATHS
A straight highway leads to the foot of ...

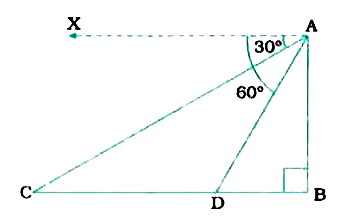
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of `30^(@)`, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be `60^(@)`. FInd the time taken by the car to reach the foot of the tower from this point.

Promotional Banner

Topper's Solved these Questions

  • APPLICATIONS OF TRIGONOMETRY

    NCERT GUJARATI|Exercise Exercise 12.1|10 Videos

  • APPLICATIONS OF TRIGONOMETRY

    NCERT GUJARATI|Exercise Exercise 12.2|10 Videos

  • COORDINATE GEOMETRY

    NCERT GUJARATI|Exercise TRY THIS|10 Videos

Similar Questions

Explore conceptually related problems

A tower stands vertically on the ground. From a point on the ground, which is 15m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60^(@) . Find the height of the tower.

From the top of a 7m high building, the angle of elevation of the top of a cable tower is 60^(@) and the angle of depression of its foot is 45^(@) . Determine the height of the tower.

The top of a clock tower is observed at engle of elevation of alpha^(@) and the feet of the tower at is the distance of d meters from the observer. Draw the diagram for this data.

The angle of elevation of the top of a tower 30m high from the foot of another tower in the same plane is 60^(@) and the angle of elevation of the top the second tower from the foot of the first tower is 30^(@) . Find the distance between the two towers and also find the height of the other tower.

From the top of a building, the angle of elevation of the top of a cell tower is 60^(@) and the angle of depression to its foot is 45^(@) . If distance of the building from the tower is 7m, then find the height ofthe tower.

The angle of elevation of the top of a building from the foot of the tower is 30^(@) and the angle of elevation of the top of the tower from the foot of the building is 60^(@) . If the tower is 50m high, find the height of the building.

From the top of a building 60m high, the angles of depression of the top and the bottom of a tower are observed to be 30^(@) and 60^(@) . Find the height of the tower.

The angle of elevation of the top of a tower at a distance 500m from the foot is 30^(@) . Then, the height of the tower is ………m.

A particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.

The angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30^(@) . Find the height of the tower.