Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-XII BOARDS-SECTIONS-C
- Two thin concentric and coplanar spherical shells, of radii a and b (b...
Text Solution
|
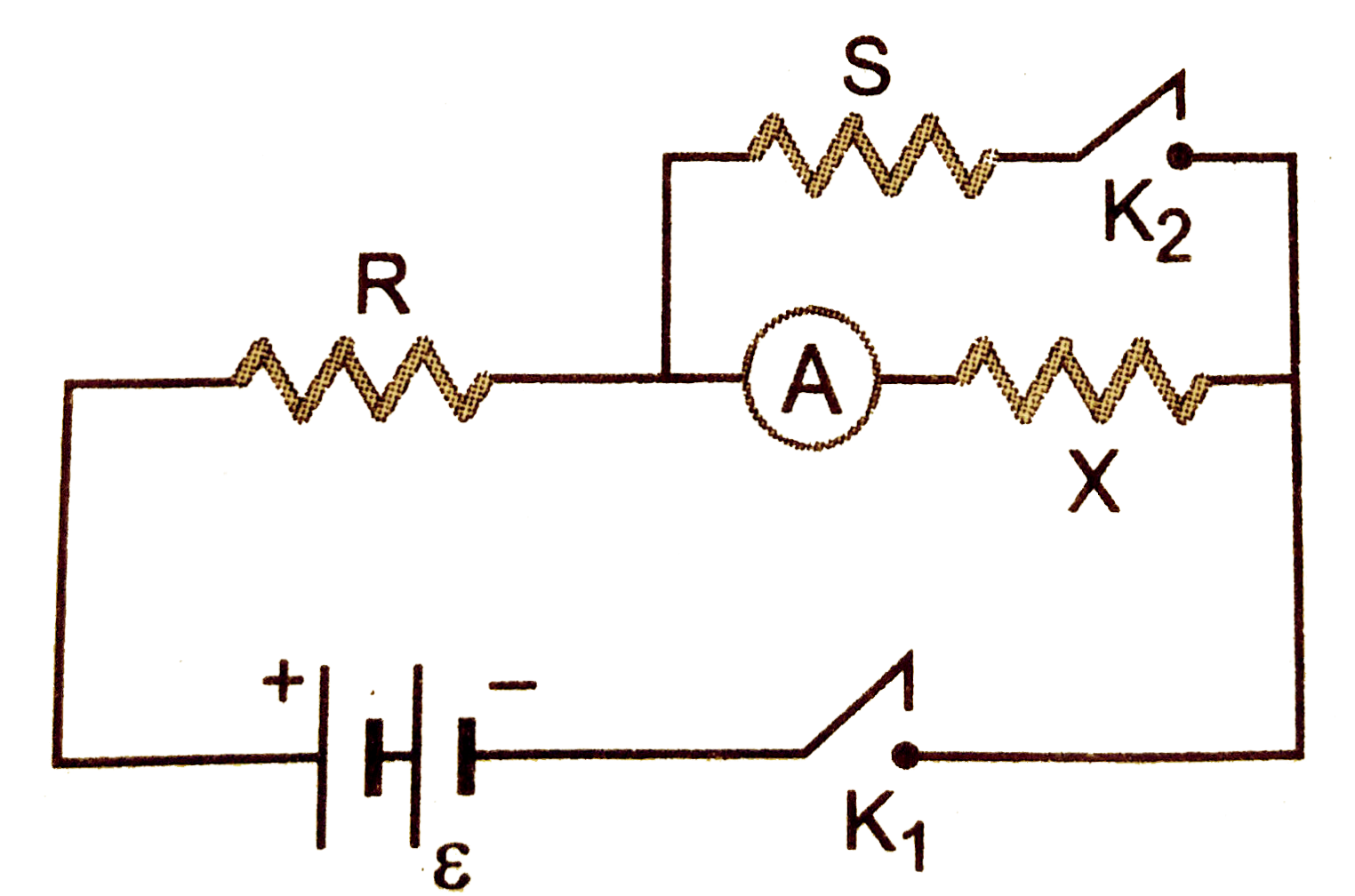
- The reading of an ammeter in the circuit (i) I when key K(1) clo...
Text Solution
|
- Three long straight parallel wires are kept as shown in figure. The wi...
Text Solution
|
- Derive the expression for the average power disspated in a series LCR ...
Text Solution
|
- Obtain the expression for the magnetic energy stored in an ideal induc...
Text Solution
|
- The graphs, drawn here, are for the phenomenon of photoelectric effect...
Text Solution
|
- Obtain the relation N=N(0)e^(-lamdat) for a sample of radio active mat...
Text Solution
|
- Given reasons for the following : (i) High reverse voltage do not ap...
Text Solution
|
- What does the term 'Modulation' used in communication system, mean ? ...
Text Solution
|
- The figure, drawn here, shows the geometry of path differences for dif...
Text Solution
|
- A circualr coil, having 100 tures of wire, of readius (nearly) 20cm ea...
Text Solution
|
- The temperature coefficient of resistance for two material A and B are...
Text Solution
|
- Two polaroids, P(1)andP(2) are set-up so that their pass-axis crossed ...
Text Solution
|